3 ベクトル空間
本章の目次
- 3.1 ベクトル空間
- 3.2 内積空間
- 3.3 一般のベクトル空間におけるノルムと直交系
- 3.4 演習問題 〜 ベクトル空間，内積空間
- 3.5 部分空間
- 3.6
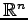の部分空間
- 3.7
![$ \mathbb{R}[x]_n$](img375.png)
の部分空間
- 3.8
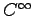の部分空間
- 3.9 演習問題 〜 部分空間
- 3.10 ベトクルの 1 次独立と 1 次従属
- 3.11 ちょっとまとめ
- 3.12 正規直交系は 1 次独立
- 3.13 ベトクルの 1 次独立の性質 〜 その 1
- 3.14 1 次結合の記法
- 3.15 ベトクルの 1 次独立の性質 〜 その 2
- 3.16 演習問題 〜 1 次独立
- 3.17 1 次独立なベクトルの最大個数
- 3.18 1 次独立なベクトルの最大個数と 1 次結合
- 3.19 1 次関係と行列の簡約化
- 3.20 1 次独立なベクトルの最大個数と行列の階数
- 3.21 1 次独立なベクトルの最大個数と行列の正則性
- 3.22 一般の場合での 1 次独立なベクトルの最大個数
- 3.23 演習問題 〜 1 次独立なベクトルの最大個数
- 3.24 ベクトルで張られる空間
- 3.25 基底
- 3.26 次元
- 3.27 ちょっとまとめ
- 3.28 ベクトルで張られる部分空間の次元
- 3.29 部分空間のさらに部分空間の次元
- 3.30 次元と同じ個数の 1 次独立なベクトルは基底
- 3.31 演習問題 〜 ベクトルで張られる空間，基底，次元
- 3.32 解空間
- 3.33 演習問題 〜 解空間
- 3.34 座標
- 3.35 基底の変換
- 3.36 座標変換
- 3.37 演習問題 〜 座標
- 3.38 正規直交基底
- 3.39 正規直交基底における座標
- 3.40 グラム・シュミットの直交化法
- 3.41 演習問題 〜 正規直交基底
- 3.42 ベクトル空間の和
- 3.43 直和分解
- 3.44 直交補空間
- 3.45 解空間の直交補空間
- 3.46 ベクトルで生成される部分空間の直交補空間
- 3.47 正規直交基底で生成される部分空間の直交補空間
- 3.48 演習問題 〜 ベクトル空間の和，直交補空間
平成20年2月2日