3.3 一般のベクトル空間におけるノルムと直交系
定義 3.11 (ノルム)
内積空間  のベクトル
のベクトル  に対して
に対して
をベクトル のノルム(norm)という.
のノルム(norm)という.
をベクトル
定義 3.12 (方向余弦)
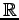 上の内積空間
上の内積空間  において
において
を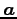 ,
, 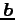 の方向余弦という.
の方向余弦という.
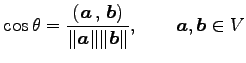 |
を
定義 3.13 (直交,直交系,正規直交系)
内積空間  において次の定義をする.
において次の定義をする.
- (i).
-
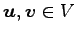 が
が
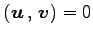 を
みたすとき
を
みたすとき 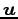 は
は 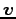 は直交するという.
は直交するという.
- (ii).
-
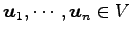 が
が
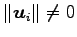 ,
,
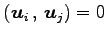 (
(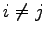 )
をみたすとき,
)
をみたすとき,
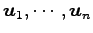 は直交系(orthogonal system)であるという.
は直交系(orthogonal system)であるという.
- (iii).
-
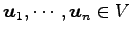 が
が
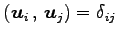 (
(
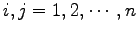 )
をみたすとき,
)
をみたすとき,
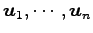 は正規直交系(orthonormal system)であるという.
は正規直交系(orthonormal system)であるという.
例 3.14 (ベクトルの内積の具体例)
ベクトル空間
![$ \mathbb{R}[x]_2$](img412.png) において内積を
において内積を
と定義する. このとき
とする. これらの内積は
となる.よって
である. また,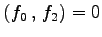 より,
より,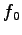 と
と 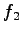 は直交する.
は直交する.
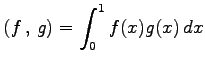 |
と定義する. このとき
とする. これらの内積は
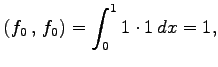 |
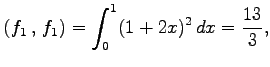 |
|||
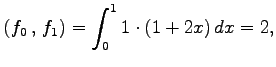 |
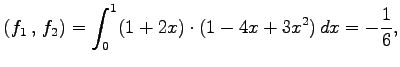 |
|||
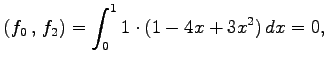 |
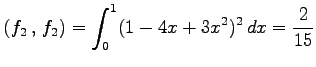 |
となる.よって
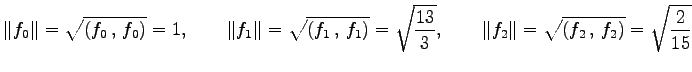 |
である. また,
問 3.15 (直交系)
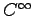 において内積を
において内積を
と定義すると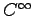 は内積空間となる.
このとき,
は内積空間となる.
このとき,
とおくと,
は直交系となる. すなわち, すべての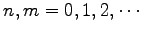 に対して
に対して
が成り立つ. これを示せ. また,正規化して正規直交系にせよ.
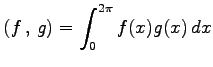 |
と定義すると
とおくと,
は直交系となる. すなわち, すべての
が成り立つ. これを示せ. また,正規化して正規直交系にせよ.
平成20年2月2日