3.2 内積空間
定義 3.3 (実ベクトル空間の内積)
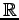 上のベクトル空間
上のベクトル空間  の任意の
2 つのベクトル
の任意の
2 つのベクトル 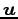 ,
, 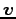 に対して,
2 項演算
に対して,
2 項演算
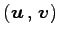 が次の条件(i)-(iv)をみたすとき,
演算
が次の条件(i)-(iv)をみたすとき,
演算
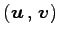 を内積(inner product)という.
を内積(inner product)という.
- (i).
-
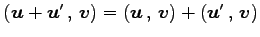 .
.
- (ii).
-
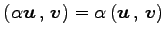 ,
,
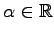 .
.
- (iii).
-
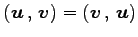 .
.
- (iv).
-
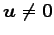 のとき
のとき
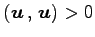 .
.
定義 3.4 (複素ベクトル空間の内積)
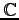 上のベクトル空間
上のベクトル空間  の任意の
2 つのベクトル
の任意の
2 つのベクトル 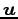 ,
, 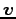 に対して,
2 項演算
に対して,
2 項演算
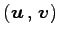 が次の条件(i)-(iv)をみたすとき,
演算
が次の条件(i)-(iv)をみたすとき,
演算
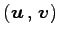 を内積(inner product)という.
を内積(inner product)という.
- (i).
-
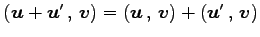 .
.
- (ii).
-
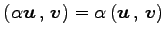 ,
,
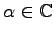 .
.
- (iii).
-
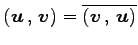 .
.
- (iv).
-
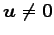 のとき
のとき
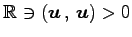 .
.
注意 3.5 (複素ベクトル空間の内積)
- (iia)
-
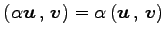 .
.
- (iib)
-
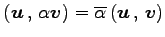 .
(
.
(
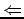 (i), (ii))
(i), (ii))
定義 3.6 (内積空間)
内積が定義されたベクトル空間を
内積空間(inner product space)という.
定義 3.7 (標準的な内積)
実ベクトル空間
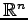 に対して内積
に対して内積
を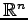 の標準的な内積という.
また,
複素ベクトル空間
の標準的な内積という.
また,
複素ベクトル空間
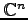 に対して内積
に対して内積
を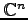 の標準的な内積という.
の標準的な内積という.
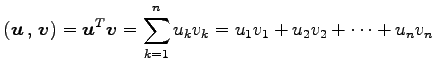 |
を
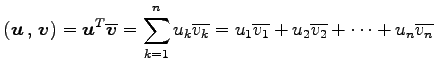 |
を
問 3.8 (標準的な内積)
標準的な内積が内積の定義(i)-(iv)をみたすことを示せ.
問 3.9 (内積の具体例)
区間 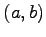 で連続関数の集合
で連続関数の集合 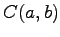 はベクトル空間である.
はベクトル空間である.
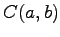 の 2 つのベクトル
の 2 つのベクトル 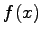 ,
, 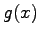 に対して 2 項演算
に対して 2 項演算
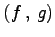 を
を
と定義する. この演算は性質(i)-(iv)をみたすので内積となる. これを示せ.
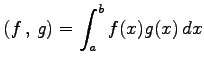 |
と定義する. この演算は性質(i)-(iv)をみたすので内積となる. これを示せ.
問 3.10 (内積の具体例)
![$ \mathbb{R}[x]_n$](img375.png) の 2 つのベクトル
の 2 つのベクトル 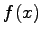 ,
, 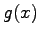 に対して 2 項演算
に対して 2 項演算
は性質(i)-(iv)をみたすので内積となる. これを示せ.
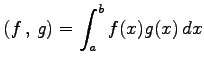 |
は性質(i)-(iv)をみたすので内積となる. これを示せ.
平成20年2月2日