3.4 演習問題 〜 ベクトル空間,内積空間
問 3.16 (ベクトル空間)
次の空間(1)-(5)がベクトル空間となるための条件
(i)
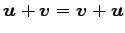 ,
(ii)
,
(ii)
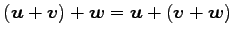 ,
(iii)
,
(iii)
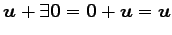 ,
(iv)
,
(iv)
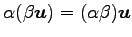 ,
(v)
,
(v)
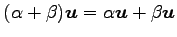 ,
(vi)
,
(vi)
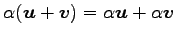 ,
(vii)
,
(vii)
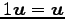 ,
(viii)
,
(viii)
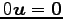 をみたすことを証明せよ.
をみたすことを証明せよ.
(1)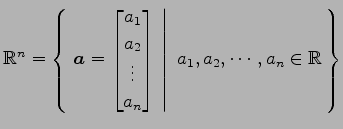 は
は
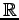 上のベクトル空間である.
上のベクトル空間である.
(2)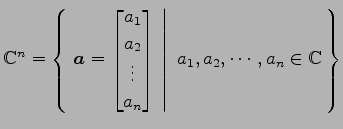 は
は
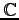 上のベクトル空間である.
上のベクトル空間である.
(3)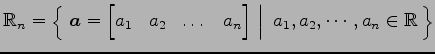 は
は
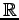 上のベクトル空間である.
上のベクトル空間である.
(4)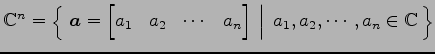 は
は
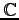 上のベクトル空間である.
上のベクトル空間である.
(5)![$ \mathbb{R}[x]_{n}=
\left\{\left.\,{f(x)=a_{0}+a_{1}x+a_{2}x^2+\cdots+a_{n}x^{n}}\,\,\right\vert\,\,{a_{0},a_{1},a_{2},\cdots,a_{n}\in\mathbb{R}}\,\right\}$](img434.png) は
は
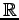 上のベクトル空間である.
上のベクトル空間である.
(1)
 は
は
(2)
 は
は
(3)
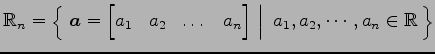 は
は
(4)
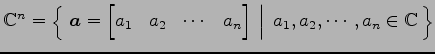 は
は
(5)
問 3.17 (内積)
次のベクトルのノルムをすべて求めよ.
また,二つのベクトルの内積とそれらの成す角を
すべての組合わせで求めよ.
(1)
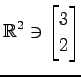 ,
,
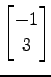 (2)
(2)
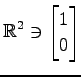 ,
,
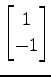 ,
,
![]() ,
,
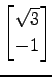 ,
,
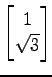 (3)
(3)
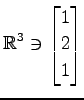 ,
,
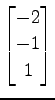 (4)
(4)
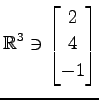 ,
,
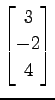 ,
,
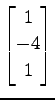 (5)
(5)
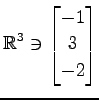 ,
,
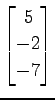 ,
,
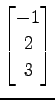
(6)
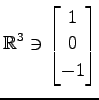 ,
,
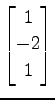 ,
,
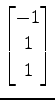 ,
,
 ,
,
![]() (7)
(7)
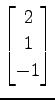
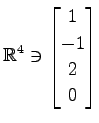 ,
,
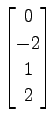 ,
,
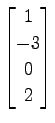 ,
,
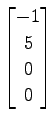
(8)
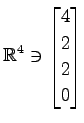 ,
,
![]() ,
,
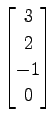 ,
,
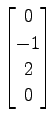 ,
,
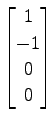 ,
,
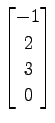 ,
,
![]() (9)
(9)
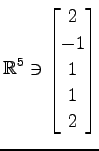 ,
,
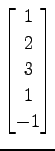
問 3.18 (内積)
次のベクトルのノルムをすべて求めよ.
また,二つのベクトルの内積を
すべての組合わせで求めよ.
(1)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
(2)
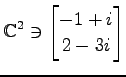 ,
,
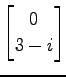 ,
,
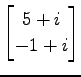 ,
,
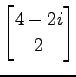 ,
,
![]()
(3)
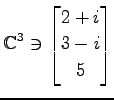 ,
,
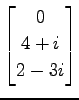 ,
,
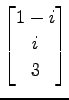 ,
,
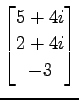 ,
,
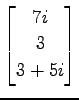
問 3.19 (内積)
次のベクトルのノルムをすべて求めよ.
また,二つのベクトルの内積とそれらの成す角を
すべての組合わせで求めよ.
ただし,内積は次のように定義する.
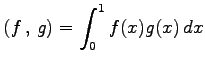 |
(1)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(2)
![]() ,
, ![]()
(3)
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
(4)
![]() ,
,
![]() ,
, ![]()
問 3.20 (直交)
次のベクトルと直交するベクトルをひとつ求めよ.
ただし,(1)-(3)の内積は標準的な内積とし,
(4)の内積は前問の内積を用いること.
(1)
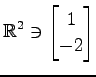 (2)
(2)
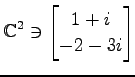 (3)
(3)
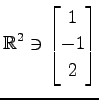 (4)
(4)
![]()
問 3.21 (直交)
ベクトル
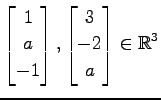 が直交するよう
が直交するよう 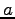 を定めよ.
を定めよ.
 が直交するよう
が直交するよう
問 3.22 (直交)
ベクトル
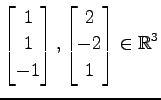 と
直交し,ノルムが
と
直交し,ノルムが  のベクトルを求めよ.
のベクトルを求めよ.
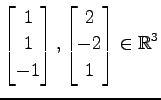 と
直交し,ノルムが
と
直交し,ノルムが
平成20年2月2日