3.5 部分空間
定義 3.23 (部分空間)
ベクトル空間  の部分集合
の部分集合  が,
が,
 と同じ和とスカラー倍の定義で,
ベクトル空間となるとき,
と同じ和とスカラー倍の定義で,
ベクトル空間となるとき,
 を
を  の部分空間(subspace)という.
の部分空間(subspace)という.
定理 3.24 (部分空間)
 の部分集合
の部分集合  が
が  の部分空間となるための
必用十分条件は次の(i)-(iii)をみたすことである.
の部分空間となるための
必用十分条件は次の(i)-(iii)をみたすことである.
- (i).
-
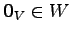 .
.
- (ii).
-
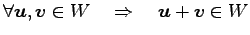 .
.
- (iii).
-
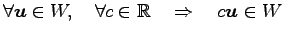 .
.
(証明)
(必用条件)
![]() が部分空間であれば,ベクトル空間の条件(i)-(viii)をみたす.
このとき条件(i)-(iii)をみたすのは明らか.
(十分条件)
が部分空間であれば,ベクトル空間の条件(i)-(viii)をみたす.
このとき条件(i)-(iii)をみたすのは明らか.
(十分条件)
![]() が条件(i)をみたすとき,ベクトル空間の条件(iii)をみたす.
条件(ii)をみたすとき,ベクトル空間の条件(i)-(ii)をみたす.
条件(iii)をみたすとき,ベクトル空間の条件(iv)-(viii)をみたす.
が条件(i)をみたすとき,ベクトル空間の条件(iii)をみたす.
条件(ii)をみたすとき,ベクトル空間の条件(i)-(ii)をみたす.
条件(iii)をみたすとき,ベクトル空間の条件(iv)-(viii)をみたす.
定理 3.25 (部分空間)
次の条件(☆)は  の部分集合
の部分集合  が
が  の部分空間となるための
必用十分条件である.
の部分空間となるための
必用十分条件である.
(証明)
![]() のとき条件(i)と等価である.
のとき条件(i)と等価である.
![]() のとき条件(ii)と等価である.
のとき条件(ii)と等価である.
![]() のとき条件(iii)と等価である.
のとき条件(iii)と等価である.
注意 3.26 (部分空間と零ベクトル)
部分空間  は零ベクトル
は零ベクトル 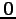 を含む.
なぜなら,
部分空間の必用十分条件(☆)で
を含む.
なぜなら,
部分空間の必用十分条件(☆)で
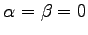 とおくと
とおくと
となるからである.
となるからである.
平成20年2月2日