3.6
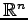 の部分空間
の部分空間
例 3.27 (部分空間の具体例)
連立方程式
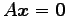 の解の集合
の解の集合
は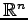 の部分集合であり,
の部分集合であり,
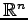 の部分空間である.
の部分空間である.
をみたすとする. このとき,
となるので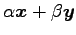 もまた解である.
よって
もまた解である.
よって
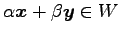 となり,
となり,
 は
は
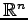 の部分空間である.
の部分空間である.
は
![]() とする.
すなわち,
とする.
すなわち,![]() ,
, ![]() は方程式
は方程式
![]() の解であり,
の解であり,
をみたすとする. このとき,
となるので
例 3.28 (部分空間の具体例)
連立方程式
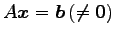 の解の集合
の解の集合
は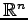 の部分集合であり,
の部分集合であり,
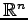 の部分空間ではない.
の部分空間ではない.
である.
は
![]() より
非同次系は原点
より
非同次系は原点 ![]() を解にもたない.
よって
を解にもたない.
よって ![]() は
は ![]() を含まず,部分空間とはならない.
つまり,
を含まず,部分空間とはならない.
つまり,
である.
例 3.29 (部分空間の具体例)
 の部分集合
の部分集合
は の部分空間である.
の部分空間である.
となる. は
は
と表される.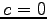 のとき
のとき
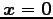 であるから
条件(i)
であるから
条件(i)
 をみたす.
ある
をみたす.
ある 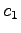 ,
, 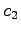 に対して
に対して
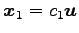 ,
,
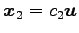 とおく.
このとき
とおく.
このとき
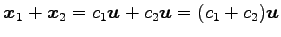 となる.任意の
となる.任意の 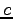 について
について 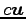 は解となるから,
は解となるから,
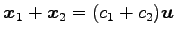 も解であるので,
条件(ii)
も解であるので,
条件(ii)
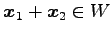 をみたす.
解
をみたす.
解
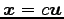 に
ある定数
に
ある定数 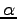 をかけた
をかけた
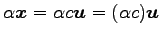 もまた解となるから,
条件(iii)
もまた解となるから,
条件(iii)
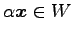 をみたす.
よって
をみたす.
よって  は部分空間である.
は部分空間である.
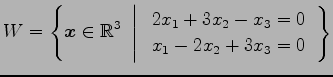 |
は
![]() は同次連立方程式の解の集合であるから,
解を求めと,
は同次連立方程式の解の集合であるから,
解を求めと,
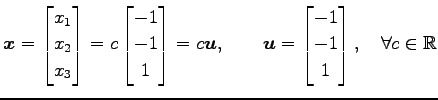 |
となる.
と表される.
例 3.30 (部分空間ではない具体例)
 の部分集合
の部分集合
は の部分空間ではない.
なぜなら,
方程式は
の部分空間ではない.
なぜなら,
方程式は
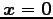 を解にもたない.
よって
を解にもたない.
よって
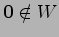 となり,
部分空間ではない.
となり,
部分空間ではない.
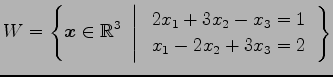 |
は
例 3.31 (部分空間ではない具体例)
集合
は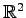 の部分空間ではない.
の部分空間ではない.
は
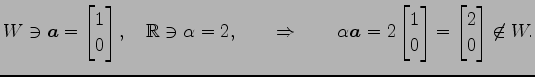 |
例 3.32 (部分空間ではない具体例)
集合
は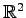 の部分空間ではない.
の部分空間ではない.
は
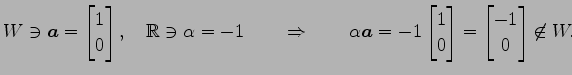 |
例 3.33 (部分空間ではない具体例)
 の部分集合
の部分集合
は の部分空間ではない.
の部分空間ではない.
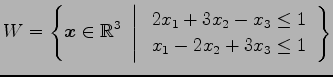 |
は
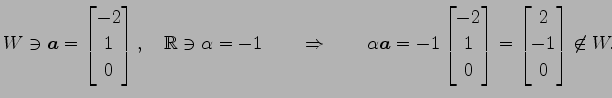 |
例 3.34 (部分空間ではない具体例)
 の部分集合
の部分集合
は の部分空間ではない.
の部分空間ではない.
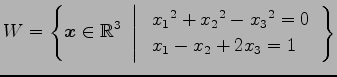 |
は
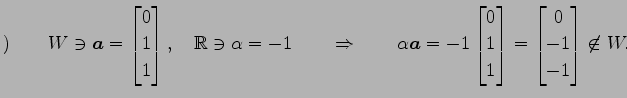 |
例 3.35 (部分空間の具体例)
 の部分集合
の部分集合
は方程式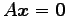 の解の集合であるから,
の解の集合であるから,
 の部分空間である.
の部分空間である.
は方程式
平成20年2月2日