3.10 ベトクルの 1 次独立と 1 次従属
定義 3.46 (1 次結合,1 次従属)
ベクトル
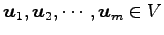 に対して,
ベクトル
に対して,
ベクトル
を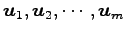 の
1 次結合または線形結合(linear combination)
という.
またこのとき,
ベクトル
の
1 次結合または線形結合(linear combination)
という.
またこのとき,
ベクトル 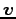 は
は
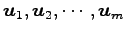 に
1 次従属または線形従属(linearly dependent)
であるという.
に
1 次従属または線形従属(linearly dependent)
であるという.
を
定義 3.47 (1 次関係,1 次独立,1 次従属)
ベクトル
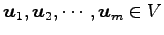 に対して,
条件式
に対して,
条件式
を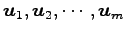 の
1 次関係または
線形関係という.
の
1 次関係または
線形関係という.
を
1 次関係をみたす係数が
![]() のみであるとき,
のみであるとき,
![]() は
1 次独立または線形独立(linearly independent)
という.
は
1 次独立または線形独立(linearly independent)
という.
![]() が
1 次独立ではないとき,
1 次従属または線形従属という.
が
1 次独立ではないとき,
1 次従属または線形従属という.
注意 3.48 (自明な 1 次関係)
任意のベクトル
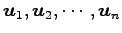 の
1 次関係
の
1 次関係
において
とおくと,明らかに 1 次関係は成立する. これを自明な 1 次関係という. 成立するのが自明な 1 次関係のみのときベクトルは 1 次独立である. また, 自明な 1 次関係ではないとき非自明な 1 次関係という. 非自明な 1 次関係のときベクトルは 1 次従属である. 非自明な場合は例えば
等々がある.
において
とおくと,明らかに 1 次関係は成立する. これを自明な 1 次関係という. 成立するのが自明な 1 次関係のみのときベクトルは 1 次独立である. また, 自明な 1 次関係ではないとき非自明な 1 次関係という. 非自明な 1 次関係のときベクトルは 1 次従属である. 非自明な場合は例えば
等々がある.
例 3.49 (ベクトルの 1 次独立,1 次従属の具体例)
ベクトル
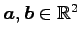 を考える.
を考える.
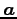 ,
, 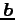 が同じ向きのときを考える.
向きが同じなので
が同じ向きのときを考える.
向きが同じなので
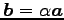 と書ける.また,
と書ける.また,
となので,非自明な 1 次関係である. よって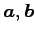 は 1 次従属である.
は 1 次従属である.
となので,非自明な 1 次関係である. よって
例 3.50 (ベクトルの 1 次独立,1 次従属の具体例)
ベクトル
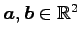 を考える.
を考える.
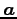 ,
, 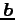 の向きが異なるときを考える.
このとき 1 次関係
の向きが異なるときを考える.
このとき 1 次関係
は自明なもののみである. もし非自明であれば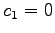 と
と 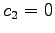 とが同時には
成立しないので,
とが同時には
成立しないので,
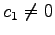 とおく.
このとき
とおく.
このとき
と表される.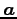 と
と 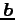 とは同じ向きとなる.
これは与えられた条件と矛盾する.
よって 1 次関係は自明なものに限る.
とは同じ向きとなる.
これは与えられた条件と矛盾する.
よって 1 次関係は自明なものに限る.
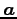 ,
, 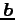 は 1 次独立である.
は 1 次独立である.
は自明なもののみである. もし非自明であれば
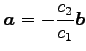 |
と表される.
例 3.51 (ベクトルの 1 次独立,1 次従属の具体例)
ベクトル
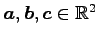 を考える.
を考える.
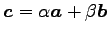 となるときを考える.
条件を書き換えると
となるときを考える.
条件を書き換えると
となる.非自明な 1 次関係であるから,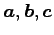 は 1 次従属である.
は 1 次従属である.
となる.非自明な 1 次関係であるから,
例 3.52 (基本ベクトルの 1 次独立性)
基本ベクトル
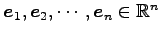 は
1 次独立である.
なぜなら, 1 次関係は
は
1 次独立である.
なぜなら, 1 次関係は
となるので,係数は自明
なものに限るからである.
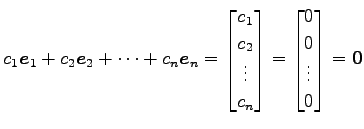 |
となるので,係数は自明
なものに限るからである.
例 3.53 (1 次独立の具体例)
![$ \mathbb{R}[x]_n$](img375.png) のベクトル
のベクトル
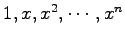 は
1 次独立なベクトルである.
は
1 次独立なベクトルである.
より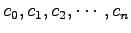 を定める.
を定める.
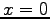 とおくと
とおくと 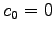 が定まる.
1 次関係を微分すると
が定まる.
1 次関係を微分すると
となる.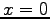 とおくと
とおくと 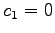 が定まる.
同様にして
が定まる.
同様にして
を得る. 自明な係数のみであるから, よって 1 次独立である.
(証明) 1 次関係
より
となる.
を得る. 自明な係数のみであるから, よって 1 次独立である.
例 3.54 (1 次独立の具体例)
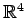 のベクトル
のベクトル
は 1 次独立であるか考える. これらの 1 次関係
をみたす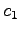 ,
, 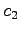 ,
, 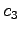 を定める.
1 次関係を変形して
を定める.
1 次関係を変形して
であり,
となり,
と表される. 行列 を簡約化すると
を簡約化すると
である.よって
を得る. 係数は自明なもの
に限るので,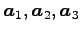 は 1 次独立である.
は 1 次独立である.
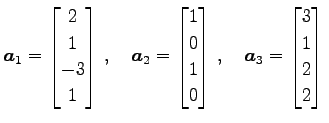 |
は 1 次独立であるか考える. これらの 1 次関係
をみたす
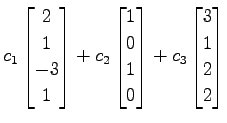 |
であり,
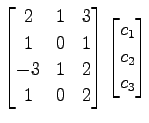 |
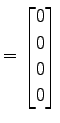 |
となり,
と表される. 行列
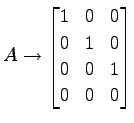 |
である.よって
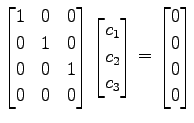 |
を得る. 係数は自明なもの
に限るので,
例 3.55 (1 次従属の具体例)
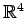 のベクトル
のベクトル
は 1 次独立であるか考える. 1 次関係より,
となる. 簡約化すると
であるから,
を得る. 1 次関係は
となる.非自明な 1 次関係であるから,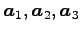 は 1 次従属である.
また,
は 1 次従属である.
また,
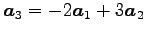 のように,
のように,
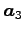 は
は 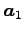 ,
, 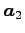 の 1 次結合で
表される.
の 1 次結合で
表される.
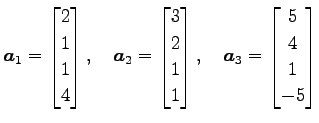 |
は 1 次独立であるか考える. 1 次関係より,
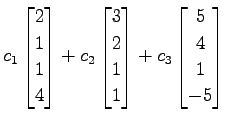 |
||
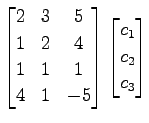 |
||
となる. 簡約化すると
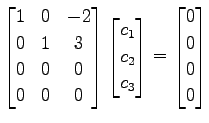 |
であるから,
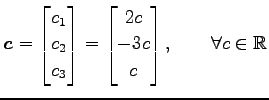 |
を得る. 1 次関係は
となる.非自明な 1 次関係であるから,
注意 3.56 (1 次従属)
一般にベクトルの組が 1 次従属のとき,
あるひとつのベクトルは他のベクトルの 1 次結合で表される.
平成20年2月2日