3.11 ちょっとまとめ
まとめ 3.57 (1 次独立性の判定)
ベクトル
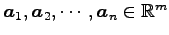 の 1 次独立性を考える.
これらのベクトルを列ベクトルにもつ行列を
の 1 次独立性を考える.
これらのベクトルを列ベクトルにもつ行列を
とおく.このとき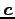 に関する方程式
に関する方程式
の解の任意定数の個数は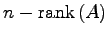 であるから,次の関係が成り立つ:
であるから,次の関係が成り立つ:
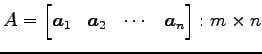 |
とおく.このとき
の解の任意定数の個数は
平成20年2月2日