3.16 演習問題 〜 1 次独立
![$\textstyle \parbox{3cm}{(1)$\,\{\vec {a},\vec {b}\}\in\mathbb{R}^2$\\
\includegraphics[width=2.5cm]{dokuritu1.eps}}$](img865.png)
![$\textstyle \parbox{3cm}{(2)$\,\{\vec {a},\vec {b}\}\in\mathbb{R}^2$\\
\includegraphics[width=2.5cm]{dokuritu2.eps}}$](img866.png)
![$\textstyle \parbox{3.3cm}{(3)$\,\{\vec {a},\vec {b},\vec {c}\}\in\mathbb{R}^2$\\
\includegraphics[width=2.5cm]{dokuritu3.eps}}$](img867.png)
![$\textstyle \parbox{3.3cm}{(4)$\,\{\vec {a},\vec {b},\vec {c}\}\in\mathbb{R}^3$\\
\includegraphics[width=2.5cm]{dokuritu4.eps}}$](img868.png)
![$\textstyle \parbox{3.8cm}{(5)$\,\{\vec {a},\vec {b},\vec {c},\vec {d}\}\in\mathbb{R}^3$\\
\includegraphics[width=2.5cm]{dokuritu5.eps}}$](img869.png)
(1)
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{3}\\ [-.5ex]{-1}\\ [-.5ex]{4}\end{bmatrix}$](img870.png) ,
,
![$ \vec{b}=\begin{bmatrix}{3}\\ [-.5ex]{8}\\ [-.5ex]{-5}\\ [-.5ex]{7}\end{bmatrix}$](img871.png) ,
,
![$ \vec{c}=\begin{bmatrix}{2}\\ [-.5ex]{9}\\ [-.5ex]{4}\\ [-.5ex]{23}\end{bmatrix}$](img872.png) (2)
(2)
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{-2}\\ [-.5ex]{4}\\ [-.5ex]{1}\end{bmatrix}$](img873.png) ,
,
![$ \vec{b}=\begin{bmatrix}{2}\\ [-.5ex]{1}\\ [-.5ex]{0}\\ [-.5ex]{-3}\end{bmatrix}$](img874.png) ,
,
![$ \vec{c}=\begin{bmatrix}{3}\\ [-.5ex]{-6}\\ [-.5ex]{1}\\ [-.5ex]{4}\end{bmatrix}$](img875.png)
(1)
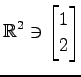 (2)
(2)
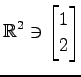 ,
,
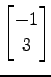 (3)
(3)
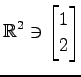 ,
,
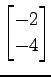 (4)
(4)
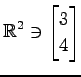 ,
,
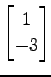
(5)
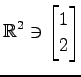 ,
,
![]() ,
,
![]() (6)
(6)
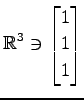 ,
,
![]() ,
,
![]() (7)
(7)
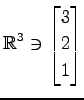 ,
,
![]() ,
,
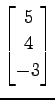
(8)
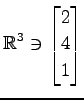 ,
,
![]() ,
,
![]() ,
,
![]() (9)
(9)
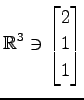 ,
,
![]() ,
,
![]() (10)
(10)
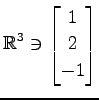 ,
,
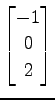
(11)
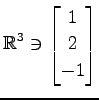 ,
,
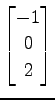 ,
,
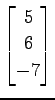 (12)
(12)
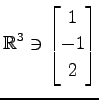 (13)
(13)
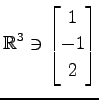 ,
,
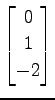
(14)
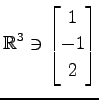 ,
,
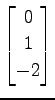 ,
,
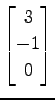 (15)
(15)
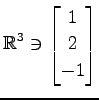 ,
,
![]() ,
,
![]() (16)
(16)
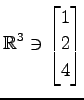 ,
,
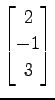 ,
,
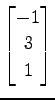
(17)
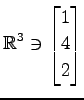 ,
,
![]() ,
,
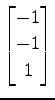 (18)
(18)
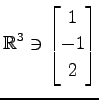 ,
,
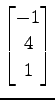 ,
,
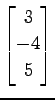 (19)
(19)
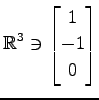 ,
,
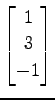 ,
,
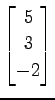
(20)
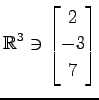 ,
,
![]() ,
,
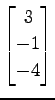 (21)
(21)
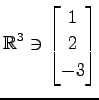 ,
,
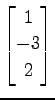 ,
,
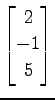
(22)
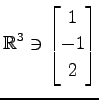 ,
,
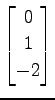 ,
,
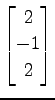 (23)
(23)
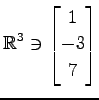 ,
,
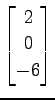 ,
,
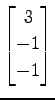 ,
,
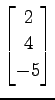
(24)
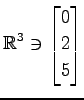 ,
,
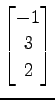 ,
,
![]() ,
,
![]() (25)
(25)
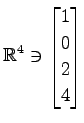 ,
,
![]() ,
,
![]() ,
,
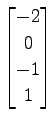
(26)
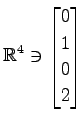 ,
,
![]() ,
,
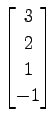 ,
,
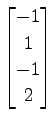 (27)
(27)
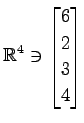 ,
,
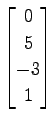 ,
,
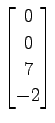
(28)
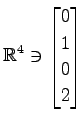 ,
,
![]() ,
,
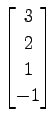 ,
,
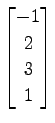 (29)
(29)
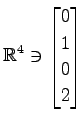 ,
,
![]()
(30)
![]()
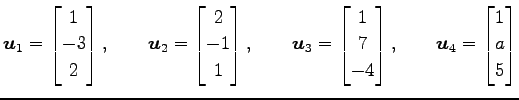 |
とおく.
(1)
(2)
(3)
(1)
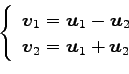 (2)
(2)
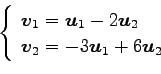 (3)
(3)
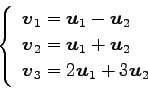
(4)
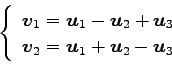 (5)
(5)
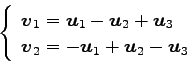 (6)
(6)
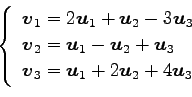
(7)
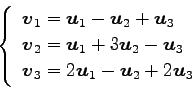 (8)
(8)
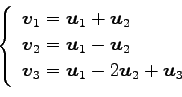 (9)
(9)
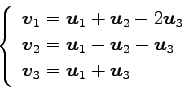 (10)
(10)
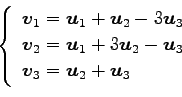 (11)
(11)
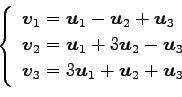 (12)
(12)
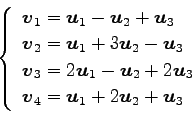 (13)
(13)
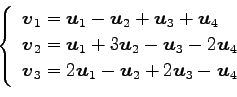 (14)
(14)
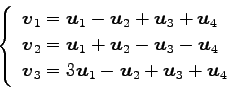
(15)
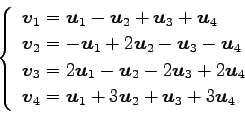 (16)
(16)
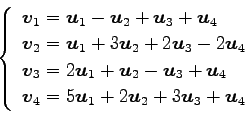
(17)
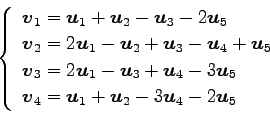 (18)
(18)
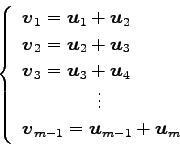 (19)
(19)
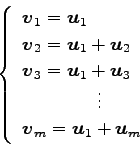
(1) 0 でない実数
(2)
平成20年2月2日