3.17 1 次独立なベクトルの最大個数
定義 3.82 (ベクトルの 1 次独立な最大個数)
ベクトルの集合 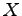 が,
ある
が,
ある 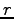 個のベクトルでは 1 次独立となり,
任意の
個のベクトルでは 1 次独立となり,
任意の 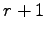 個のベクトルでは 1 次従属となるとき,
個のベクトルでは 1 次従属となるとき,
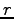 を集合
を集合 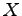 の
1 次独立なベクトルの最大個数という.
の
1 次独立なベクトルの最大個数という.
定理 3.83 (ベクトルの 1 次独立な最大個数)
ベクトルの集合
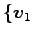 ,
, 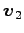 ,
,  ,
,
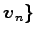 ,
,
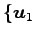 ,
, 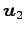 ,
,  ,
,
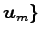 において,
において,
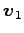 ,
,  ,
, 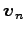 の各ベクトルが
の各ベクトルが
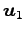 ,
,  ,
, 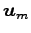 の 1 次結合で表されるとき,
の 1 次結合で表されるとき,
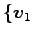 ,
, ,
,
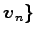 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
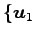 ,
, ,
,
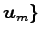 の
1 次独立なベクトルの最大個数以下となる.
の
1 次独立なベクトルの最大個数以下となる.
であり,
と書ける.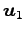 ,
,  ,
, 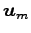 の 1 次独立のベクトルの最大個数を
の 1 次独立のベクトルの最大個数を 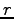 とする.
とする.
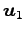 ,
,  ,
, 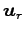 が 1 次独立であるとすると,
その他のベクトル
が 1 次独立であるとすると,
その他のベクトル
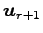 ,
,  ,
, 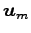 は
は
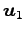 ,
,  ,
, 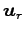 の 1 次結合で表される.
よって
の 1 次結合で表される.
よって
と表される. このとき
となる. これより
を得る.よって
となる.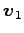 ,
,  ,
, 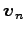 の
各ベクトルは
の
各ベクトルは 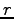 個のベクトル
個のベクトル
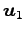 ,
,  ,
, 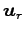 の
1 次結合で表される.
このとき
の
1 次結合で表される.
このとき
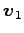 ,
,  ,
, 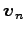 のうち
任意の
のうち
任意の 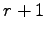 個のベクトルは 1 次従属であるので,
1 次独立の最大個数は
個のベクトルは 1 次従属であるので,
1 次独立の最大個数は 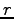 個以下となる.
個以下となる.
(証明)
![]() ,
, ![]() ,
, ![]() の各ベクトルは
の各ベクトルは
![]() ,
, ![]() ,
, ![]() の 1 次結合で表されるので
の 1 次結合で表されるので
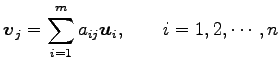 |
であり,
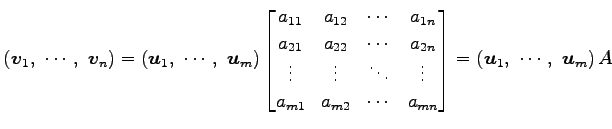 |
と書ける.
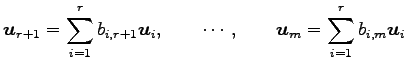 |
と表される. このとき
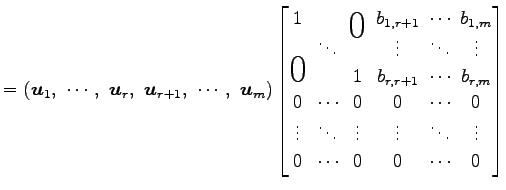 |
||
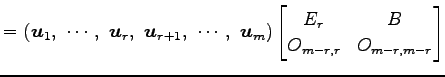 |
となる. これより
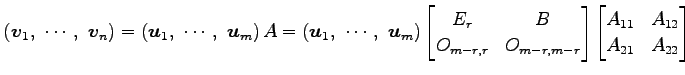 |
||
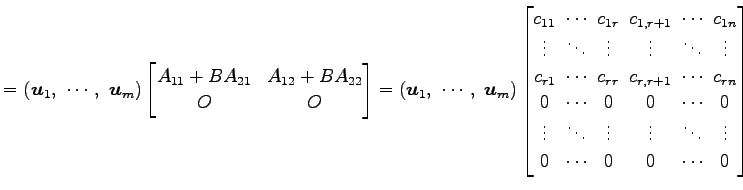 |
を得る.よって
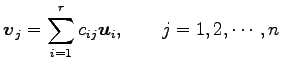 |
となる.
例 3.84 (ベクトルの 1 次独立な最大個数の具体例)
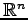 の 1 次独立なベクトルの最大個数は
の 1 次独立なベクトルの最大個数は 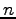 である.
である.
を 1 次独立と仮定する. このとき 1 次関係
を考える. これより
となる. 係数行列の階数は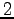 以下であるから
以下であるから
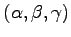 は任意定数を含む解であり,
1 次関係は非自明係数となる.
よって,
は任意定数を含む解であり,
1 次関係は非自明係数となる.
よって,
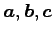 は
1 次従属である.
以上より,
は
1 次従属である.
以上より,
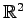 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は 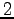 である.
である.
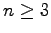 のときも同様に示される.
のときも同様に示される.
(証明)
![]() のときを考える.
まず明らかに
のときを考える.
まず明らかに
![]() は 1 次独立であるので,
1 次独立なベクトルの最大個数は 2 以上である.
ここで,3 個のベクトル
は 1 次独立であるので,
1 次独立なベクトルの最大個数は 2 以上である.
ここで,3 個のベクトル
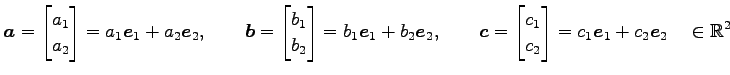 |
を 1 次独立と仮定する. このとき 1 次関係
を考える. これより
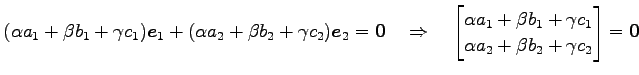 |
||
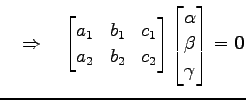 |
となる. 係数行列の階数は
平成20年2月2日