3.18 1 次独立なベクトルの最大個数と 1 次結合
定理 3.85 (ベクトルの 1 次独立な最大個数)
ベトクルの集合
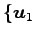 ,
, 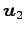 ,
,  ,
,
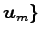 の 1 次独立なベクトルの最大個数が
の 1 次独立なベクトルの最大個数が 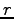 であることの必用十分条件は,
であることの必用十分条件は,
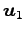 ,
,  ,
, 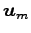 のなかに
のなかに 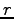 個の 1 次独立な
ベクトルがあり,
他の
個の 1 次独立な
ベクトルがあり,
他の 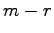 個のベクトルはこの
個のベクトルはこの 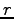 個のベクトルの 1 次結合で
表されることである.
個のベクトルの 1 次結合で
表されることである.
と表されるから,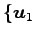 ,
,  ,
,
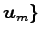 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
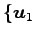 ,
,  ,
,
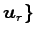 の
1 次独立なベクトルの最大個数
の
1 次独立なベクトルの最大個数 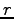 以下となる.
よって
以下となる.
よって
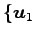 ,
,  ,
,
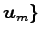 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は 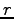 である.
である.
(証明)
(必用条件)
![]() ,
, ![]() ,
, ![]() のうち
1 次独立な
のうち
1 次独立な ![]() 個のベクトルを
個のベクトルを
![]() ,
, ![]() ,
, ![]() とする.
このとき
とする.
このとき ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(
![]() ) は 1 次従属であるから,
) は 1 次従属であるから,
![]() は
は
![]() ,
, ![]() ,
, ![]() の 1 次結合で表される.
(十分条件)
の 1 次結合で表される.
(十分条件)
![]() 個のベクトル
個のベクトル ![]() ,
, ![]() ,
, ![]() が 1 次独立であるとする.
が 1 次独立であるとする.
![]() ,
, ![]() ,
,
![]() の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は ![]() 以上となる.
また,
他の
以上となる.
また,
他の ![]() 個のベクトル
個のベクトル
![]() ,
, ![]() ,
,
![]() が
が
![]() ,
, ![]() ,
, ![]() の 1 次結合で表されるとする.
このとき,
の 1 次結合で表されるとする.
このとき,
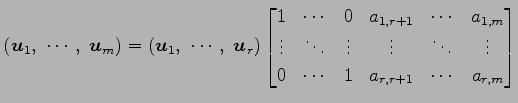 |
と表されるから,
例 3.86 (ベクトルの 1 次独立な最大個数の具体例)
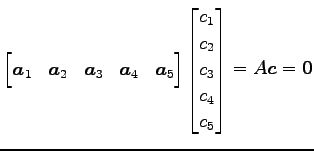
ベクトル
の 1 次独立なベクトルの最大個数と そのときベクトルの組の一つを求める. また,その他のベクトルを 1 次独立なベクトルの 1 次結合で表す.
を考える.これは
と表される. 方程式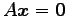 の解を求めることで,
1 次関係の係数
の解を求めることで,
1 次関係の係数 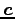 が定まる.
行列
が定まる.
行列 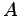 を簡約化すると
を簡約化すると
となる. 方程式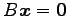 の解と
方程式
の解と
方程式
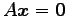 の解とは等しく
の解とは等しく 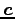 であるから,
ベクトル
であるから,
ベクトル
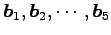 の 1 次関係と
ベクトル
の 1 次関係と
ベクトル
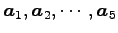 の 1 次関係は等しい.
の 1 次関係は等しい.
であり, の基本ベクトルである.
明らかに
ベクトルの組
の基本ベクトルである.
明らかに
ベクトルの組
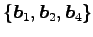 は 1 次独立であるので,
1 次独立なベクトルの最大個数は
は 1 次独立であるので,
1 次独立なベクトルの最大個数は 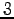 以上である.
他のベクトル
以上である.
他のベクトル
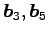 について見ると
について見ると
が成り立つ.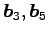 はそれぞれ
はそれぞれ
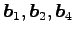 に
関して 1 次従属である.
に
関して 1 次従属である.
となる. この方程式の係数行列は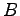 そのものであるから,
階数は
そのものであるから,
階数は 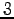 であり非自明な係数をもつ.
よって
であり非自明な係数をもつ.
よって
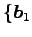 ,
, 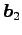 ,
,
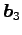 ,
, 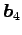 ,
,
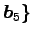 は
1 次従属となる.
次に
は
1 次従属となる.
次に 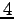 個のベクトルの組が 1 次従属となることを示す.
個のベクトルの組が 1 次従属となることを示す.
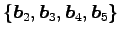 ,
,
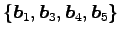 ,
,
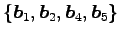 ,
,
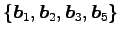 ,
,
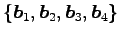 の
1 次関係は同様の操作で,
の
1 次関係は同様の操作で,
とそれぞれなる. これらの方程式の係数行列はそれぞれ 行列 の第
の第  ,
,  ,
, 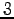 ,
, 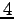 ,
, 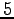 列目を除いた形をしている.
係数行列の階数はいずれも
列目を除いた形をしている.
係数行列の階数はいずれも 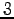 以下であるから,
非自明な 1 次関係が存在する.
以下であるから,
非自明な 1 次関係が存在する.
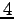 個のベクトルの組はいずれも 1 次従属となる.
(その 2)
また別の方法としては次のように示す.
方程式
個のベクトルの組はいずれも 1 次従属となる.
(その 2)
また別の方法としては次のように示す.
方程式
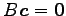 の解は,
任意定数を
の解は,
任意定数を 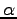 ,
, 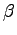 とすると
とすると
と表される.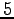 個のベクトルの組
個のベクトルの組
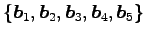 の 1 次関係は(☆)である.
非自明な 1 次関係であるから
の 1 次関係は(☆)である.
非自明な 1 次関係であるから
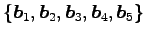 は
1 次従属となる.
また,(○)より
は
1 次従属となる.
また,(○)より
と非自明な 1 次関係が成り立つので, ベクトルの組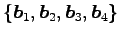 ,
,
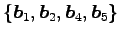 は 1 次従属となる.
さらには(☆)において,
は 1 次従属となる.
さらには(☆)において,
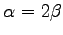 ,
,
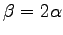 ,
, 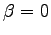 とおくと,
それぞれ
とおくと,
それぞれ
と非自明な 1 次関係が成り立つので,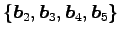 ,
,
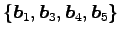 ,
,
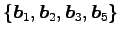 は
1 次従属となる.
は
1 次従属となる.
として表される.
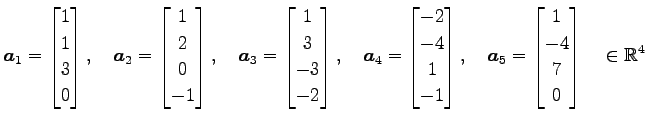 |
の 1 次独立なベクトルの最大個数と そのときベクトルの組の一つを求める. また,その他のベクトルを 1 次独立なベクトルの 1 次結合で表す.
まず,
ベクトル
![]() の 1 次関係
の 1 次関係
を考える.これは
 |
と表される. 方程式
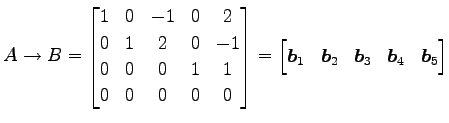 |
となる. 方程式
まず,
![]() の
1 次独立なベクトルの最大個数を考える.
の
1 次独立なベクトルの最大個数を考える.
![]() に着目すると,
に着目すると,
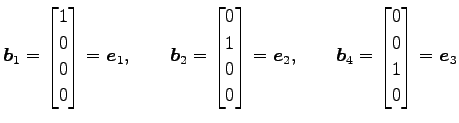 |
であり,
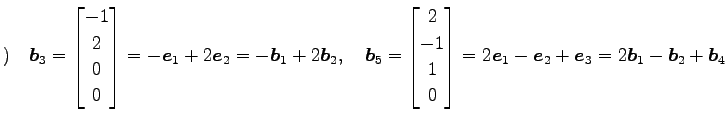 |
が成り立つ.
![]() 個以上のベクトルの組が 1 次従属となることを示す.
(その 1)
まず,
個以上のベクトルの組が 1 次従属となることを示す.
(その 1)
まず,![]() 個の
ベクトルの組
個の
ベクトルの組
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() に関する 1 次関係は(○)を用いると
に関する 1 次関係は(○)を用いると
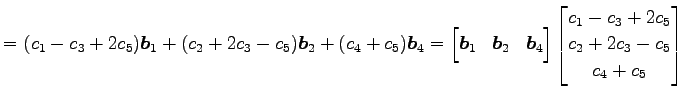 |
||
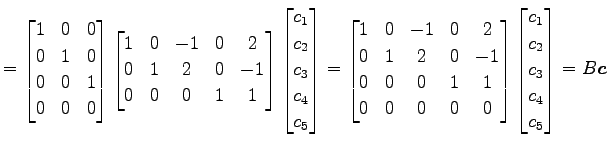 |
となる. この方程式の係数行列は
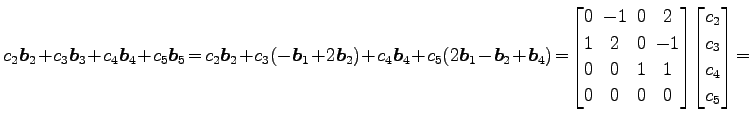 |
||
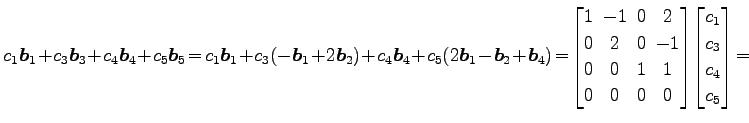 |
||
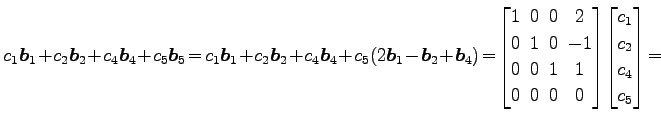 |
||
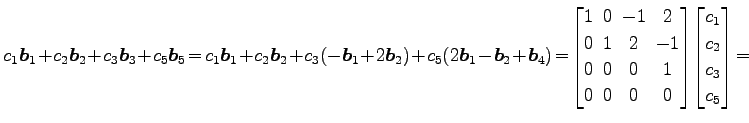 |
||
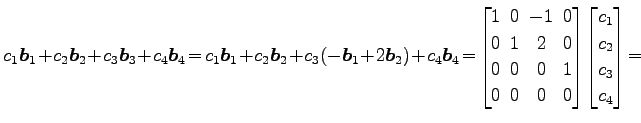 |
とそれぞれなる. これらの方程式の係数行列はそれぞれ 行列
と表される.
と非自明な 1 次関係が成り立つので, ベクトルの組
と非自明な 1 次関係が成り立つので,
以上より,ベクトルの組
![]() の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
![]() である.
これらの結果は
ベクトル
である.
これらの結果は
ベクトル
![]() の
1 次関係にも適用される.
1 次独立なベクトルの最大個数は
の
1 次関係にも適用される.
1 次独立なベクトルの最大個数は
![]() であり,
その 1 次独立となるベクトルの組のひとつは
であり,
その 1 次独立となるベクトルの組のひとつは
![]() である.
また,その他のベクトルはこれらの 1 次結合
である.
また,その他のベクトルはこれらの 1 次結合
として表される.
平成20年2月2日