3.19 1 次関係と行列の簡約化
定理 3.87 (簡約化行列の 1 次関係)
行列
を簡約化した行列を
とする. このとき の列ベクトル
の列ベクトル
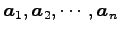 に関する
1 次関係と
に関する
1 次関係と 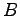 の列ベクトル
の列ベクトル
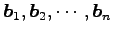 に関する
1 次関係とは等価である.
に関する
1 次関係とは等価である.
と表される. これは
となるので,各列ベクトルは
と表される.また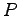 は正則行列であるから,
は正則行列であるから,
とも表される. ここで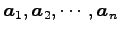 に関する
1 次関係を
に関する
1 次関係を
とする.これより,
を得る. これは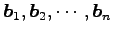 に関する 1 次関係であり,
に関する 1 次関係であり,
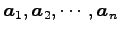 に関する 1 次関係と
等しい.
に関する 1 次関係と
等しい.
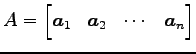 |
を簡約化した行列を
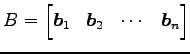 |
とする. このとき
(証明)
行列 ![]() を簡約化して
を簡約化して ![]() となるとき,
基本変形を表す行列
となるとき,
基本変形を表す行列 ![]() を用いて
を用いて
と表される. これは
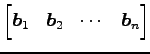 |
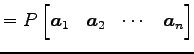 |
|
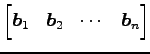 |
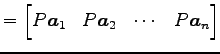 |
となるので,各列ベクトルは
と表される.また
とも表される. ここで
とする.これより,
を得る. これは
平成20年2月2日