3.20 1 次独立なベクトルの最大個数と行列の階数
定理 3.88 (行列の列ベクトルと行ベクトルの 1 次独立な最大個数)
となるとする.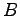 の零ベクトルではない行ベクトルの個数を
の零ベクトルではない行ベクトルの個数を 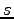 とする.
このときベクトル
とする.
このときベクトル 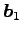 ,
,  ,
, 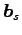 の
1 次関係は
の
1 次関係は
であり,自明な係数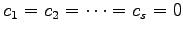 のみであるから,
のみであるから,
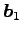 ,
,  ,
, 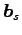 は 1 次独立である.
よって
は 1 次独立である.
よって
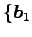 ,
,  ,
,
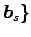 の 1 次独立な
ベクトルの最大個数は
の 1 次独立な
ベクトルの最大個数は
 である.
次に,
である.
次に,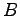 は
は  を基本変形を繰り返して得られるので,
を基本変形を繰り返して得られるので,
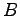 の行ベクトルすべては
の行ベクトルすべては  の行ベクトルの 1 次結合
の行ベクトルの 1 次結合
で表される.よって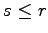 が成り立つ.
一方,
が成り立つ.
一方,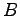 に対して基本変形を繰り返して
に対して基本変形を繰り返して  を得ることもできるので,
を得ることもできるので,
と表される.よって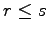 が成り立つ.
以上より,
が成り立つ.
以上より,
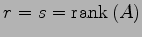 が得られる.
が得られる.
(証明)
行列 ![]() を列ベクトルに分割し,
を列ベクトルに分割し,
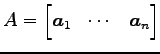 とおく.
行列
とおく.
行列 ![]() を簡約化し,
を簡約化し,
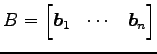 を得たとする.
を得たとする.
![]() とすると,
ベクトル
とすると,
ベクトル ![]() ,
, ![]() ,
, ![]() のうちで
主成分がある列ベクトルは,
左から順に基本ベクトル
のうちで
主成分がある列ベクトルは,
左から順に基本ベクトル ![]() ,
, ![]() ,
, ![]() となる.
主成分がない他の列ベクトルは基本ベクトル
となる.
主成分がない他の列ベクトルは基本ベクトル
![]() ,
, ![]() ,
, ![]() の 1 次結合で表される.
基本ベクトルは明らかに 1 次独立であるから,
の 1 次結合で表される.
基本ベクトルは明らかに 1 次独立であるから,
![]() ,
, ![]() ,
,
![]() の 1 次独立なベクトルの
最大個数は
の 1 次独立なベクトルの
最大個数は ![]() となる.
となる.
![]() ,
, ![]() ,
,
![]() の 1 次関係は
の 1 次関係は
![]() ,
, ![]() ,
,
![]() の 1 次関係と等しいので,
の 1 次関係と等しいので,
![]() ,
, ![]() ,
,
![]() の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は ![]() となる.
となる.
行列 ![]() を行ベクトルに分割し簡約化して
を行ベクトルに分割し簡約化して
![$\displaystyle A= \begin{bmatrix}\vec{a}_1 \\ \vdots \\ \vec{a}_m \end{bmatrix} ...
...ex] \vec{b}_s \\ [-1ex] \vec{0}\\ [-1ex] \vdots \\ [-1ex] \vec{0} \end{bmatrix}$](img1090.png) |
となるとする.
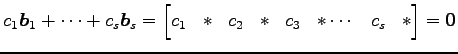 |
であり,自明な係数
で表される.よって
と表される.よって
平成20年2月2日