3.46 ベクトルで生成される部分空間の直交補空間
定理 3.200 (直交補空間の次元)
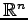 の部分空間
の部分空間
の次元は
である. 一方, の直交補空間
の直交補空間 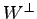 は
方程式
は
方程式
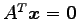 の解空間であり,
の解空間であり,
となり,次元は
である.
と表される.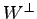 の元
の元  は
は
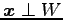 であり
であり
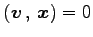 をみたす.
これより,
をみたす.
これより,
となる.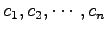 は任意の実数であるから,
は任意の実数であるから,
が成り立つ. これは
であり,
と表される. よって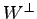 は方程式
は方程式
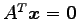 の解空間である.
の解空間である.
の次元は
 |
である. 一方,
となり,次元は
である.
(証明)
![]() の任意のベクトルは
の任意のベクトルは
と表される.
となる.
が成り立つ. これは
であり,
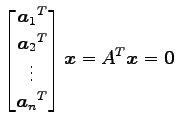 |
と表される. よって
例 3.201 (直交補空間の具体例)
 における部分空間
における部分空間
の直交補空間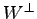 を求める.
を求める.
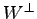 の任意のベクトルを
の任意のベクトルを  とする.
とする.
 は
は  の任意のベクトル
の任意のベクトル
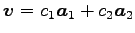 と
直交するので
と
直交するので
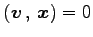 が成り立つ.
こりより,
が成り立つ.
こりより,
と表される. すべての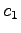 ,
, 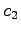 について成り立つためには
について成り立つためには
をみたさなければならない. この連立方程式を書き直すと
であり,
となる. これを解く. 係数行列を簡約化すると
となるので,解は
となる. よって,直交補空間は
と得られる.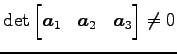 より
より
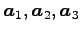 は 1 次独立である.
よって
は 1 次独立である.
よって
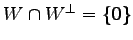 であるので,
であるので,
が成り立つ. また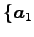 ,
, 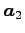 ,
,
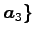 は
は
 の
基底となることに注意する.
つまり
の
基底となることに注意する.
つまり
である.
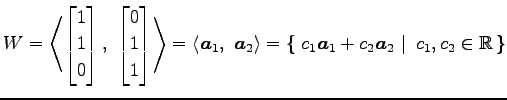 |
の直交補空間
と表される. すべての
をみたさなければならない. この連立方程式を書き直すと
であり,
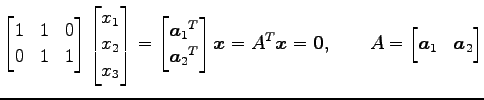 |
となる. これを解く. 係数行列を簡約化すると
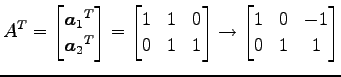 |
となるので,解は
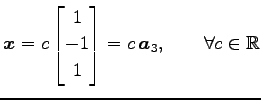 |
となる. よって,直交補空間は
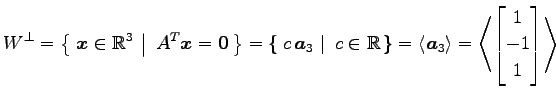 |
と得られる.
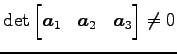 より
より
が成り立つ. また
である.
平成20年2月2日