3.36 座標変換
定理 3.146 (座標変換)
ベクトル空間 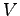 のベクトル
のベクトル 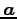 に対して,
基底
に対して,
基底
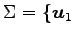 ,
,
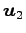 ,
,  ,
,
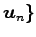 に
おける座標が
に
おける座標が
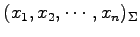 であり,
基底
であり,
基底
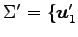 ,
,
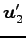 ,
,  ,
,
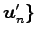 に
おける座標が
に
おける座標が
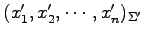 であるとする.
また,
基底
であるとする.
また,
基底 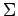 に対する基底
に対する基底 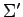 の変換行列が
の変換行列が 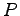 であるとする.
すなわち
であるとする.
すなわち 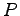 は
は
をみたすとする. このとき,
が成立する. これを 座標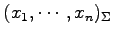 から
座標
から
座標
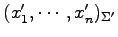 への
座標変換(coordinate transformation)という.
への
座標変換(coordinate transformation)という.
となる. 基底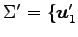 ,
,
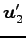 ,
,  ,
,
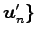 のとき
の座標が
のとき
の座標が
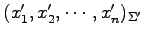 であれば
であれば
となる. これらのベクトルは等しいので,
と表される. ここで, 基底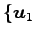 ,
,
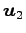 ,
,  ,
,
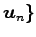 に対する
基底
に対する
基底
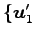 ,
,
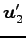 ,
,  ,
,
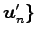 の
変換行列を
の
変換行列を 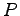 とおくとき,
とおくとき,
が成り立つので,
を得る. これより,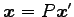 が成り立つ.
が成り立つ.
をみたすとする. このとき,
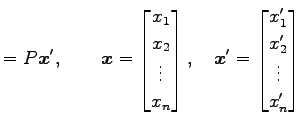 |
が成立する. これを 座標
(証明)
ベクトル空間 ![]() の任意のベクトル
の任意のベクトル ![]() を考える.
基底
を考える.
基底
![]() ,
,
![]() ,
, ![]() ,
,
![]() のとき
の座標が
のとき
の座標が
![]() であれば
であれば
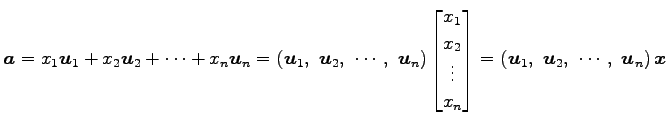 |
となる. 基底
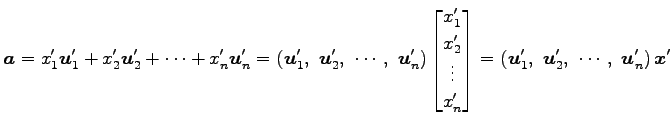 |
となる. これらのベクトルは等しいので,
と表される. ここで, 基底
が成り立つので,
を得る. これより,
例 3.147 (座標変換の具体例)
 の点
の点
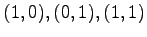 は,
標準基底
は,
標準基底
における座標で表すと,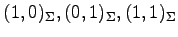 と
表される.
これらの点を
基底
と
表される.
これらの点を
基底
における座標として表す. 基底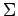 から基底
から基底 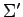 への座標変換を考える.
基底
への座標変換を考える.
基底 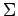 に対する基底
に対する基底 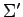 の変換行列を
の変換行列を 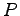 とおくと,
とおくと,
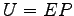 より
より
となる. このとき座標変換は
と表される. 点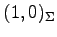 ,
,
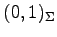 ,
,
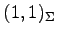 より
より
とおく. このとき座標変換より
と表される. よって 座標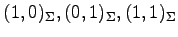 は
それぞれ
は
それぞれ
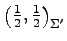 ,
,
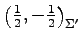 ,
,
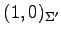 となる.
となる.
を座標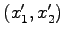 で表す.(☆)を代入すると
で表す.(☆)を代入すると
を得る.
における座標で表すと,
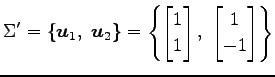 |
における座標として表す. 基底
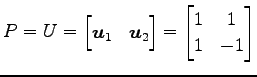 |
となる. このとき座標変換は
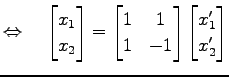 |
![$\displaystyle \Leftrightarrow\quad \left\{ \begin{array}{l} x_1=x'_1+x'_2 \\ [1ex] x_2=x'_1-x'_2 \end{array}\right.$](img1632.png) |
|||||
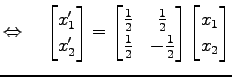 |
![$\displaystyle \Leftrightarrow\quad \left\{ \begin{array}{l} \displaystyle{x'_1=...
...(x_1+x_2)} \\ [1ex] \displaystyle{x'_2=\frac{1}{2}(x_1-x_2)} \end{array}\right.$](img1635.png) |
と表される. 点
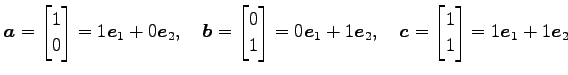 |
とおく. このとき座標変換より
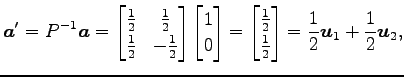 |
||
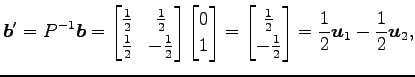 |
||
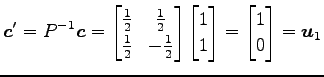 |
と表される. よって 座標
また,座標 ![]() における直線
における直線
を座標
を得る.
例 3.148 (座標変換の具体例)
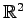 において 2 組の基底
において 2 組の基底
とあるベクトル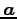 を考える.
を考える.
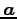 の基底
の基底 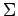 における
座標が
における
座標が
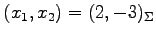 のとき,
のとき,
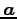 は
は
となる. ベクトル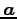 の基底
の基底 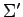 における
座標
における
座標
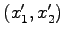 を求める.
ここで,
を求める.
ここで,
より,座標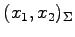 から
座標
から
座標
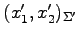 への
座標変換
への
座標変換
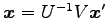 を得る.
座標
を得る.
座標
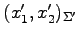 を得るためには
を得るためには
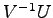 を左から掛けて
を左から掛けて
を用いる. これに数値を代入すると, ベクトル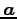 の基底
の基底 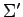 における
座標が
における
座標が
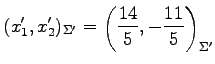 と得られる.
と得られる.
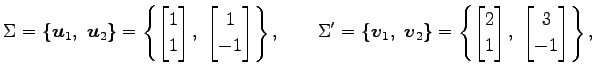 |
とあるベクトル
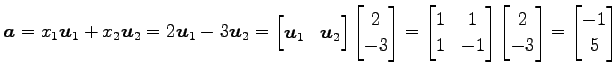 |
となる. ベクトル
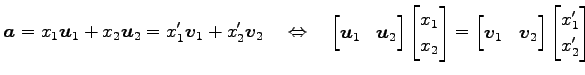 |
||
より,座標
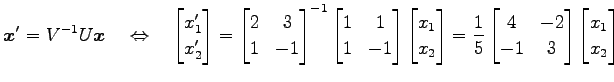 |
を用いる. これに数値を代入すると, ベクトル
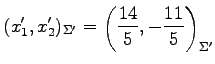 と得られる.
と得られる.
例 3.149 (座標変換の具体例)
![$ \mathbb{R}[x]_2$](img412.png) のベクトル
のベクトル  の
基底
の
基底
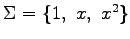 における
座標が
における
座標が
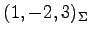 のとき,
基底
のとき,
基底
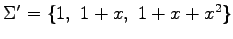 における
座標
における
座標
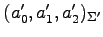 を求める.
まず,
を求める.
まず, は
は
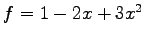 であり,
であり,
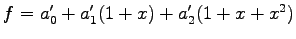 と書ける.
これらが等しいので,
と書ける.
これらが等しいので,
が成り立つ.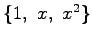 は 1 次独立であるから,
方程式
は 1 次独立であるから,
方程式
を得る.これを解くと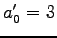 ,
, 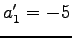 ,
, 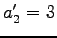 となる.
よって
となる.
よって
と表され,基底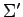 における
における  の座標は
の座標は
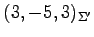 となる.
となる.
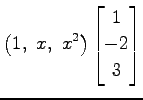 |
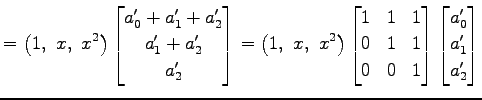 |
が成り立つ.
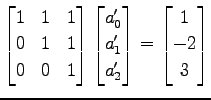 |
を得る.これを解くと
と表され,基底
平成20年2月2日