3.35 基底の変換
ベクトル空間の基底の取り方は一意ではないので,
あるベクトル空間 ![]() に対して
に対して
が成り立つ. ここで
と書ける. ここで
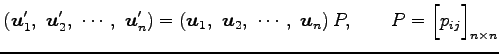 |
とも表される.
定義 3.140 (基底の変換行列)
ベクトル空間  の基底
の基底
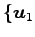 ,
,
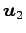 ,
,  ,
,
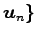 と基底
と基底
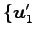 ,
,
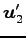 ,
,  ,
,
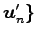 に対して
に対して
をみたす行列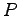 を基底の変換行列という.
を基底の変換行列という.
をみたす行列
注意 3.141 (基底の変換行列)
数ベクトル空間(
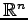 または
または
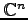 )における
基底の変換は
)における
基底の変換は
とも表される.
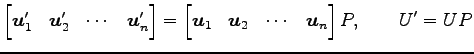 |
とも表される.
注意 3.142 (基底の変換行列の正則性)
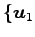 ,
,  ,
,
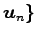 と
と
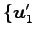 ,
,  ,
,
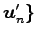 は
1 次独立であるから,
基底の変換行列
は
1 次独立であるから,
基底の変換行列 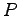 は正則である.
は正則である.
例 3.143 (基底の変換行列の具体例)
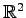 において
標準基底
において
標準基底
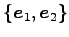 から
基底
から
基底
への変換行列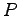 を求める.
を求める.
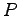 は
は
をみたす.
とおくと
となる. よって
を得る.
をみたすので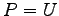 を得る.
を得る.
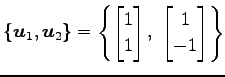 |
への変換行列
をみたす.
方法 1: まず,
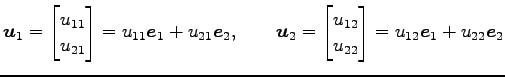 |
とおくと
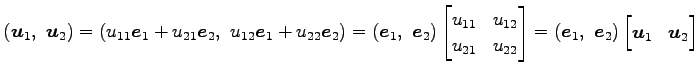 |
となる. よって
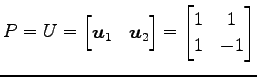 |
を得る.
方法 2:
または,![]() は
は
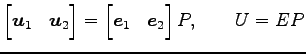 |
をみたすので
定理 3.144 (基底の変換行列)
ベクトル空間  において,
基底
において,
基底
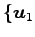 ,
,  ,
,
 から
基底
から
基底
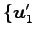 ,
,  ,
,
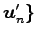 への
変換行列を
への
変換行列を 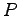 とし,
基底
とし,
基底
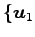 ,
,  ,
,
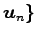 から
基底
から
基底
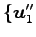 ,
,  ,
,
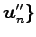 への
変換行列を
への
変換行列を 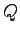 とする.
このとき
基底
とする.
このとき
基底
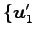 ,
,  ,
,
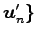 から
基底
から
基底
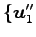 ,
,  ,
,
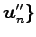 への
変換行列
への
変換行列 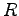 は
は
である.
が成り立つ.これより
となるので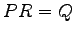 を得る.
よって
を得る.
よって 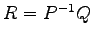 となる.
となる.
である.
(証明) まず,定義より
が成り立つ.これより
となるので
例 3.145 (基底の変換行列の具体例)
 において基底
において基底
に対する基底
への変換行列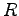 を求める.
すなわち,
を求める.
すなわち,
をみたす行列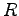 を求める.
を求める.
が成立する. このとき
となるので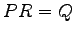 より
より
を得る.
をみたすので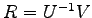 より得られる.
より得られる.
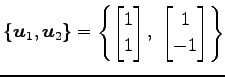 |
に対する基底
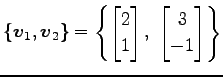 |
への変換行列
をみたす行列
方法 1:
まず,標準基底
![]() に対する
基底
に対する
基底
![]() と
と
![]() の変換行列を
の変換行列を ![]() ,
, ![]() とおく.
すなわち,
とおく.
すなわち,
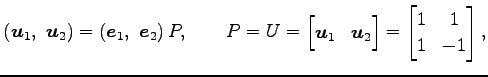 |
||
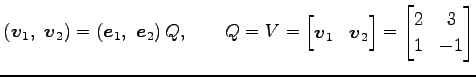 |
が成立する. このとき
となるので
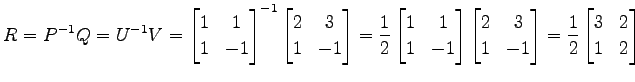 |
を得る.
方法 2:
または,![]() は
は
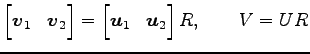 |
をみたすので
平成20年2月2日