3.28 ベクトルで張られる部分空間の次元
定理 3.113 (ベクトル空間の次元と階数)
部分空間
の次元は
である.
となる.このとき の任意のベクトルは
の任意のベクトルは
である. よって の基底は
の基底は
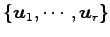 となり,
次元は
となり,
次元は
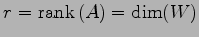 となる.
となる.
の次元は
 |
である.
(証明)
ベクトル
![]() の
1 次独立なベクトル最大個数は
の
1 次独立なベクトル最大個数は
![]() である.
である.
![]() ,
, ![]() ,
, ![]() が 1 次独立であるとすると,
その他のベクトル
が 1 次独立であるとすると,
その他のベクトル
![]() ,
, ![]() ,
, ![]() は
これらの 1 次結合で表されるので,
は
これらの 1 次結合で表されるので,
となる.このとき
である. よって
例 3.114 (部分空間の次元の具体例)
ベクトル
で生成される の部分空間
の部分空間
を考える.この次元を求める.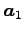 ,
, 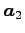 ,
, 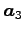 を列ベクトルする
行列
を列ベクトルする
行列  を簡約化して
を簡約化して
を得る. このとき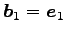 ,
,
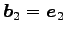 ,
,
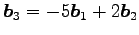 が成り立つので,
が成り立つので,
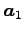 ,
, 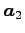 は 1 次独立であり,
は 1 次独立であり,
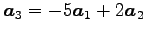 が成り立つ.
ベクトルの組
が成り立つ.
ベクトルの組
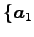 ,
, 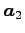 ,
,
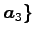 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
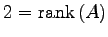 である.
である.
 の任意のベクトルは
の任意のベクトルは
と表される.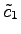 ,
,
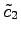 は任意であるから
は任意であるから
が成り立つ.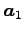 ,
, 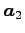 は 1 次独立であるから,
は 1 次独立であるから,
 の基底は
の基底は
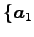 ,
,
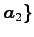 となる.
よって
となる.
よって
を得る.
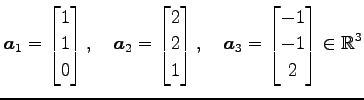 |
で生成される
を考える.この次元を求める.
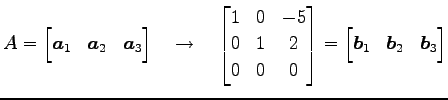 |
を得る. このとき
と表される.
が成り立つ.
を得る.
平成20年2月2日