3.43 直和分解
定義 3.188 (直和分解)
ベクトル空間  とその部分空間
とその部分空間 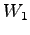 ,
, 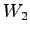 が
が
をみたすとき, を
を 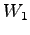 と
と 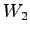 に直和分解するという.
に直和分解するという.
をみたすとき,
例 3.189 (直和分解の具体例)
ベクトル
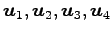 を 1 次独立とする.
このとき
を 1 次独立とする.
このとき
が成り立ち, は直和分解される.
は直和分解される.
が成り立ち,
平成20年2月2日
3.43 直和分解
定義 3.188 (直和分解) ベクトル空間とその部分空間
,
が
をみたすとき,を
と
に直和分解するという.
例 3.189 (直和分解の具体例) ベクトルを 1 次独立とする. このとき
が成り立ち,は直和分解される.
平成20年2月2日