3.44 直交補空間
定義 3.190 (ベクトルと部分空間の直交)
内積空間  において,
ベクトル
において,
ベクトル
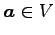 と
部分空間
と
部分空間  に含まれる
すべてのベクトル
に含まれる
すべてのベクトル 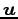 とが直交するとき,
すなわち
とが直交するとき,
すなわち
が成り立つとき,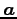 と
と  とは直交するといい,
とは直交するといい,
と表記する.
が成り立つとき,
と表記する.
例 3.191 (ベクトルと部分空間とが直交する具体例)
 の部分空間
の部分空間
とベクトル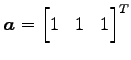 と
は直交
と
は直交
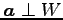 する.
なぜなら,方程式
する.
なぜなら,方程式
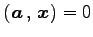 の
解空間が
の
解空間が  であるからである.
この例では
であるからである.
この例では  は平面であり
は平面であり 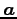 は
は  の法線ベクトルである.
の法線ベクトルである.
とベクトル
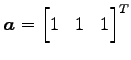 と
は直交
と
は直交
また,
ベクトル
![]() (
(
![]() ) も
) も
![]() をみたすので,
直線
をみたすので,
直線
![]() 上のすべてのベクトルに対して,
上のすべてのベクトルに対して,
![]() が成り立つ.
が成り立つ.
![]() に直交するベクトルは 1 通りではないことに注意する.
に直交するベクトルは 1 通りではないことに注意する.
定義 3.192 (直交補空間)
内積空間  とその部分空間
とその部分空間  に対して,
部分空間
に対して,
部分空間
を における
における  の直交補空間という.
の直交補空間という.
を
定理 3.193 (直交補空間は部分空間)
直交補空間 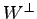 は
は  の部分空間である.
の部分空間である.
問 3.194 (直交補空間は部分空間)
これを示せ.
定理 3.195 (直交補空間による直和分解)
内積空間  における部分空間
における部分空間  の直交補空間
の直交補空間 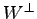 は
は
をみたす.次元は
の関係が成り立つ.
をみたす.次元は
の関係が成り立つ.
例 3.196 (直交補空間の具体例)
 の部分空間
の部分空間
の直交補空間は
である.このとき,
が成り立つ.
の直交補空間は
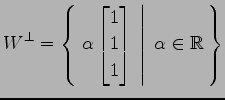 |
である.このとき,
が成り立つ.
例 3.197 (直交補空間の具体例)
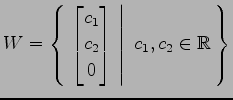
 における部分空間
における部分空間
の直交補空間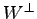 は
は
である. なぜなら, 任意のベクトル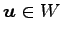 ,
,
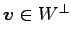 に対して
に対して
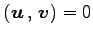 が成り立つからである.
が成り立つからである.
 |
の直交補空間
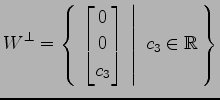 |
である. なぜなら, 任意のベクトル
平成20年2月2日