3.14 1 次結合の記法
定義 3.63 ( 1 次結合の記法)
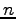 個のベクトル
個のベクトル 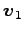 ,
, 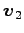 ,
,  ,
,
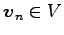 のそれぞれが,
のそれぞれが,
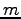 個のベクトル
個のベクトル 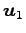 ,
, 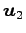 ,
,  ,
,
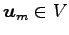 の 1 次結合として,
の 1 次結合として,
と表されるとする.このとき,
と表記することにする.
と表されるとする.このとき,
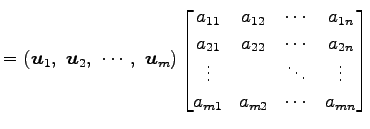 |
||
と表記することにする.
例 3.64 ( 1 次結合の記法)
ベクトル 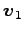 ,
, 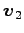 ,
,
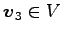 と
と
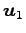 ,
,
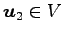 が
が
をみたすとき,
と表される.
をみたすとき,
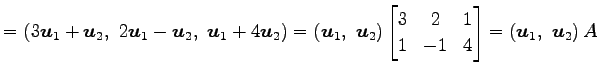 |
と表される.
注意 3.65 (1 次結合の記法)
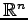 または
または
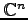 において,前例のベクトルは
において,前例のベクトルは
と行列として表されることに注意する.
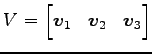 |
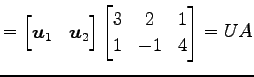 |
と行列として表されることに注意する.
例 3.66 (1 次結合の記法)
ベクトル
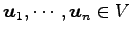 の 1 次関係は
の 1 次関係は
と表される.
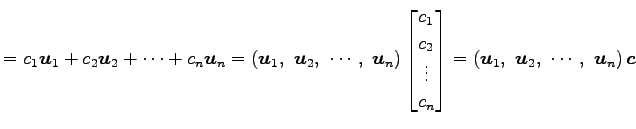 |
と表される.
平成20年2月2日