3.13 ベトクルの 1 次独立の性質 〜 その 1
定理 3.59 (1 次独立の性質)
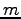 個の
ベトクル
個の
ベトクル
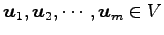 に対して
次の条件が成り立つ.
に対して
次の条件が成り立つ.
をみたす非自明な係数 が存在する.
このとき,
が存在する.
このとき,
となるので,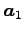 ,
,  ,
, 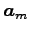 は 1 次従属である.
(ii)は(i)の対偶である.
は 1 次従属である.
(ii)は(i)の対偶である.
- (i).
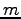 個のうち
個のうち
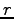
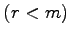 個のベクトル
個のベクトル
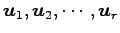 が
1 次従属であれば,
が
1 次従属であれば,
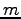 個のベトクル
個のベトクル
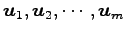 も
1 次従属となる.
も
1 次従属となる.
- (ii).
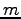 個のベトクル
個のベトクル
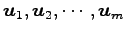 が
1 次独立であれば,
が
1 次独立であれば,
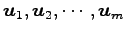 のうち
任意の
のうち
任意の 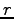
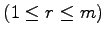 個のベクトルも 1 次独立である.
個のベクトルも 1 次独立である.
(証明)
(i) ベクトル ![]() ,
, ![]() ,
, ![]() は
1 次従属であるので, 1 次関係
は
1 次従属であるので, 1 次関係
をみたす非自明な係数
となるので,
定理 3.60 (1 次独立の性質)
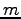 個のベクトル
個のベクトル 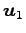 ,
, 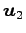 ,
,  ,
, 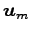 が
1 次従属であることと,
が
1 次従属であることと,
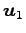 ,
, 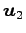 ,
,  ,
, 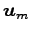 のうち
少なくとも 1 個のベクトルが
他の
のうち
少なくとも 1 個のベクトルが
他の 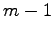 個のベクトルの 1 次結合で表されることとは,
必用十分条件である.
個のベクトルの 1 次結合で表されることとは,
必用十分条件である.
をみたす係数で非自明なもの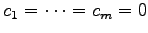 以外にも存在する.
例えば
以外にも存在する.
例えば 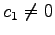 とすると
とすると
となる.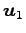 は
は
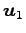 ,
,  ,
, 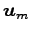 の 1 次結合で表される.
(十分条件)
の 1 次結合で表される.
(十分条件)
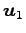 が他のベクトル
が他のベクトル
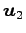 ,
,  ,
, 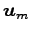 の 1 次結合で表されるとすると
の 1 次結合で表されるとすると
となる.これより
を得る.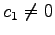 であるから,
非自明な係数
であるから,
非自明な係数
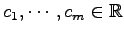 が存在する.
よって
が存在する.
よって
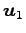 ,
,  ,
, 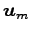 は 1 次従属である.
は 1 次従属である.
(証明)
(必用条件)
ベクトル ![]() ,
, ![]() ,
, ![]() が 1 次従属であれば,
1 次関係
が 1 次従属であれば,
1 次関係
をみたす係数で非自明なもの
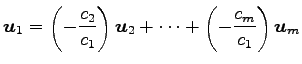 |
となる.
となる.これより
を得る.
定理 3.61 (1 次独立の性質)
ベトクル
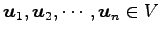 が
1 次独立のとき,
あるベクトル
が
1 次独立のとき,
あるベクトル
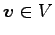 が
が
と表されるとする. このとき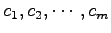 は一意に定まる.
は一意に定まる.
と書かれる. これらの差をとると
となる. これは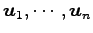 に関する 1 次関係である.
に関する 1 次関係である.
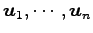 は 1 次独立であるから,
は 1 次独立であるから,
であり,
が成り立つ. 係数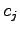 は一意に定まる.
は一意に定まる.
と表されるとする. このとき
(証明) 一意に表されないと仮定する. このとき
と書かれる. これらの差をとると
となる. これは
であり,
が成り立つ. 係数
定理 3.62 (1 次独立の性質)
ベクトル
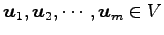 が 1 次独立であり,
が 1 次独立であり,
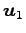 ,
, 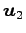 ,
,  ,
, 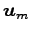 ,
,
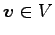 が 1 次従属とする.
このとき
が 1 次従属とする.
このとき
と一意に表される.
の係数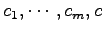 は非自明なものとなる.
このとき
は非自明なものとなる.
このとき 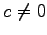 となる.
なぜなら
となる.
なぜなら 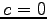 とすると
係数
とすると
係数
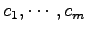 のうち
のうち 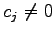 となる係数が
存在することになり,
1 次関係
となる係数が
存在することになり,
1 次関係
は非自明な係数が存在することになる. これはベクトル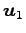 ,
, 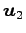 ,
,  ,
, 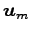 が
1 次独立であることと矛盾する.
よって
が
1 次独立であることと矛盾する.
よって 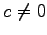 となる.
このときベクトル
となる.
このときベクトル 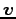 は
は
と一意に表される.
と一意に表される.
(証明)
ベクトル ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() は 1 次従属であるから,
1 次関係
は 1 次従属であるから,
1 次関係
の係数
は非自明な係数が存在することになる. これはベクトル
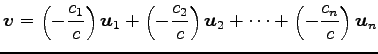 |
と一意に表される.
平成20年2月2日