3.33 �齬���� �� �����
�� 3.135 (�����)
���β���֤δ���ȼ�������补
��������(12), (13), (19)�Ǥ�
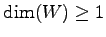 �Ȥʤ�褦
�Ȥʤ�褦 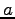 ���ͤ����补
���ͤ����补
(1)
![]() (2)
(2)
![]()
(3)
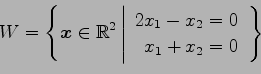 (4)
(4)
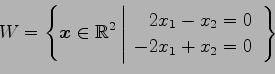
(5)
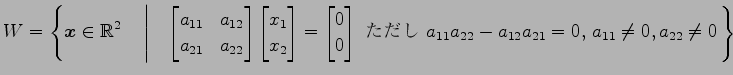
(6)
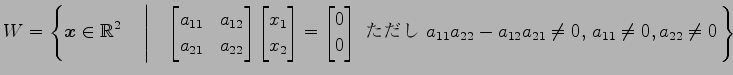
(7)
![]() (8)
(8)
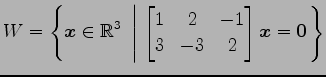
(9)
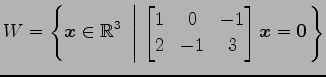 (10)
(10)
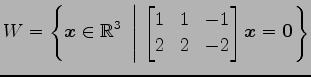
(11)
 (12)
(12)
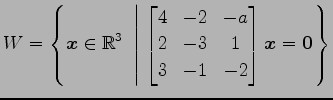
(13)
 (14)
(14)

(15)
 (16)
(16)
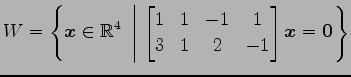
(17)
 (18)
(18)
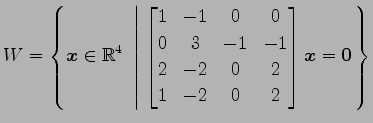
(19)
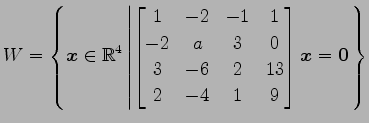 (20)
(20)
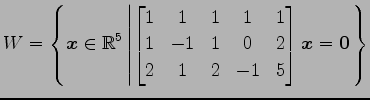
(21)

(22)
![]() (23)
(23)
![]()
ʿ��20ǯ2��2��