3.32 解空間
定義 3.129 (解空間)
同次方程式
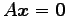 の解の集合
の解の集合
を解空間(solution space)という.
を解空間(solution space)という.
定理 3.130 (解空間と部分空間)
解空間  は
は
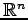 の部分空間である.
の部分空間である.
をみたすとする. このとき,
となるので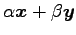 もまた解である.
よって
もまた解である.
よって
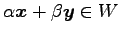 となり,
となり,
 は
は
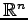 の部分空間である.
の部分空間である.
(証明)
![]() とする.
すなわち,
とする.
すなわち,![]() ,
, ![]() は方程式
は方程式
![]() の解であり,
の解であり,
をみたすとする. このとき,
となるので
注意 3.131 (非同次系の解空間)
非同次方程式
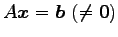 の
解集合
の
解集合  は
は
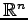 の部分空間ではない.
なぜなら,
の部分空間ではない.
なぜなら,
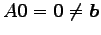 より
原点
より
原点 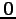 を解にもたない.
よって
を解にもたない.
よって
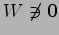 であり,
部分空間とはならない.
であり,
部分空間とはならない.
定義 3.132 (一般解)
解空間  の基底
の基底
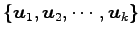 を
方程式
を
方程式
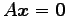 の基本解という.
このとき
の基本解という.
このとき  の任意のベクトルは
基本解の線形結合で
の任意のベクトルは
基本解の線形結合で
と表される. これを方程式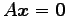 の
一般解(general solution)という.
の
一般解(general solution)という.
と表される. これを方程式
定理 3.133 (解空間の次元)
同次系の解空間
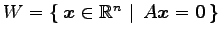 の次元は解の任意定数の個数と等しく,
の次元は解の任意定数の個数と等しく,
で与えられる.
の形で得たとする. ただし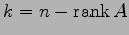 とおく.
このときベクトルの組
とおく.
このときベクトルの組
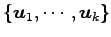 が
1 次独立か調べる.
これらの 1 次関係は
が
1 次独立か調べる.
これらの 1 次関係は
となる. 行列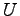 は必ず
は必ず
の形をしているので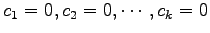 が成り立つ.
よってベクトルの組
が成り立つ.
よってベクトルの組
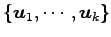 は
1 次独立である.
このとき解空間
は
1 次独立である.
このとき解空間  は
は
となるので の基底は
の基底は
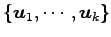 である.
よって
である.
よって
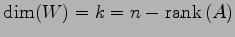 となる.
となる.
で与えられる.
(証明)
行列 ![]() を簡約化して
方程式
を簡約化して
方程式
![]() の解を
の解を
の形で得たとする. ただし
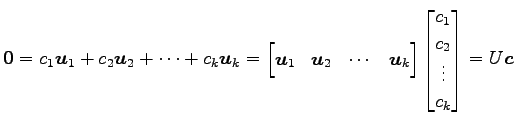 |
となる. 行列
![$\displaystyle U= \begin{bmatrix}* & * & * & \cdots & * \\ [-1ex] 1 & 0 & 0 & \c...
...\\ [-1ex] * & * & * & \cdots & * \\ [-1ex] * & * & * & \cdots & * \end{bmatrix}$](img1490.png) |
の形をしているので
となるので
例 3.134 (解空間の具体例)
解空間
を考える. 方程式を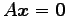 とおく.
とおく.
 を簡約化して
を簡約化して
となる. これより,方程式は
と書き換わる.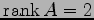 より任意定数の個数は
より任意定数の個数は
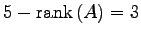 となり,
任意定数を
となり,
任意定数を
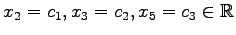 とおく.
よって一般解は
とおく.
よって一般解は
と得られる. ここで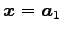 ,
,
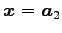 ,
,
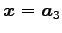 は基本解である.
解空間は
は基本解である.
解空間は
となる. の基底を求める.
の基底を求める.
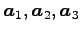 が 1 次独立であるか調べる.
1 次関係
が 1 次独立であるか調べる.
1 次関係
は
となる. よって条件をみたすのは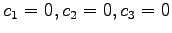 のときのみである.
のときのみである.
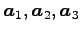 は 1 次独立である.
は 1 次独立である.
 の基底は
の基底は
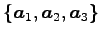 となる.
以上より
となる.
以上より
を得る. これは解の任意定数の個数と等しい.
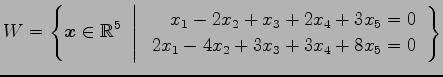 |
を考える. 方程式を
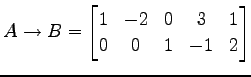 |
となる. これより,方程式は
と書き換わる.
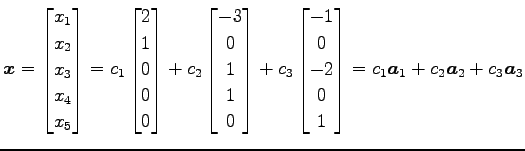 |
と得られる. ここで
となる.
は
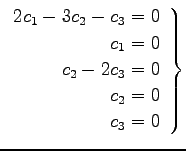 |
となる. よって条件をみたすのは
を得る. これは解の任意定数の個数と等しい.
平成20年2月2日