3.26 次元
定理 3.103 (ベクトル空間の基底の個数)
ベクトル空間の基底の個数は取り方に依らず一意に定まる.
その個数は,
ベクトル空間に含まれる 1 次独立なベクトルの最大個数と等しい.
(証明)
ベトクル
![]() と
と
![]() が
共に
が
共に ![]() の基底とする.
このとき,
の基底とする.
このとき,
![]() は
は
![]() の 1 次結合で書ける.
の 1 次結合で書ける.
![]() と仮定すると
と仮定すると
![]() は 1 次従属であり,
は 1 次従属であり,
![]() が 1 次独立であることと矛盾する.
よって
が 1 次独立であることと矛盾する.
よって ![]() である.
同様に
である.
同様に
![]() は
は
![]() の 1 次結合で書ける.
の 1 次結合で書ける.
![]() と仮定すると
と仮定すると
![]() は 1 次従属であり,
は 1 次従属であり,
![]() が 1 次独立であることと矛盾する.
よって
が 1 次独立であることと矛盾する.
よって ![]() である.以上より
である.以上より ![]() となり,
基底の個数は一定である.
となり,
基底の個数は一定である.
定義 3.104 (次元)
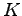 上のベクトル空間
上のベクトル空間 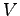 の基底の個数が
の基底の個数が 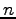 個であるとき,
これをベクトル空間
個であるとき,
これをベクトル空間 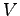 の次元(dimension)と呼び,
の次元(dimension)と呼び,
と表記する. または省略して単に
と表記する.
と表記する. または省略して単に
と表記する.
注意 3.105 (零ベクトル空間)
零ベクトル 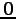 のみからなるベクトル空間
のみからなるベクトル空間
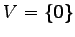 を
零ベクトル空間といい,
次元は
を
零ベクトル空間といい,
次元は 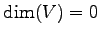 とする.
とする.
定義 3.106 (有限次元のベクトル空間)
ベクトル空間 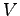 の次元
の次元 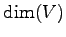 が有限であるとき,
が有限であるとき,
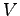 を有限次元のベクトル空間という.
を有限次元のベクトル空間という.
定理 3.107 (ベクトル空間の次元)
ベクトル空間 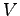 の次元
の次元 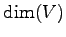 は
は
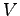 の 1 次独立なベクトルの最大個数と等しい.
の 1 次独立なベクトルの最大個数と等しい.
(証明)
(必用条件)
![]() とすると,
基底の個数は
とすると,
基底の個数は ![]() である.
このとき任意の
である.
このとき任意の ![]() 個以上のベクトルは 1 次従属となるから,
個以上のベクトルは 1 次従属となるから,
![]() の 1 次独立なベクトルの最大個数は
の 1 次独立なベクトルの最大個数は ![]() である.
(十分条件)
である.
(十分条件)
![]() の 1 次独立なベクトルの最大個数を
の 1 次独立なベクトルの最大個数を ![]() とする.
とする.
![]() ,
, ![]() ,
, ![]() が 1 次独立とすると,
が 1 次独立とすると,
![]() ,
, ![]() ,
, ![]() ,
, ![]() は 1 次従属となる.
このとき
は 1 次従属となる.
このとき ![]() は
は
![]() ,
, ![]() ,
, ![]() の 1 次結合で表される.
これは
の 1 次結合で表される.
これは
![]() は
は ![]() の任意のベクトルに対して成り立つので,
の任意のベクトルに対して成り立つので,
![]() ,
, ![]() ,
,
![]() は
は ![]() の基底となる.
よって
の基底となる.
よって ![]() を得る.
を得る.
例 3.108 (ベクトル空間の次元の具体例)
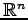 は
は
と表される. 標準基底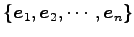 の
個数は
の
個数は 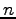 である.
よって次元は
である.
よって次元は
となる.
と表される. 標準基底
となる.
例 3.109 (ベクトル空間の次元の具体例)
![$ \mathbb{R}[x]_n$](img375.png) の次元を考える.
の次元を考える.
![$ \mathbb{R}[x]_n$](img375.png) のベクトル
のベクトル 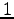 ,
, 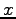 ,
, 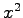 ,
,  ,
, 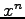 の
1 次関係
の
1 次関係
の係数は自明なもの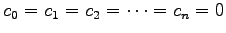 に限るので,
に限るので,
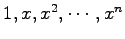 は 1 次独立である.
また,このベクトルの 1 次結合全体の集合は
は 1 次独立である.
また,このベクトルの 1 次結合全体の集合は
をみたす.よって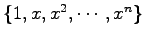 は
は
![$ \mathbb{R}[x]_n$](img375.png) の基底となるから,
の基底となるから,
となる.
の係数は自明なもの
をみたす.よって
となる.
例 3.110 (ベクトル空間の次元の具体例)
無限回微分可能な関数全体の集合
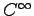 は
は
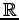 上のベクトル空間である.
上のベクトル空間である.
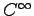 は解析関数
は解析関数
全体の集合であるから, 基底として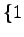 ,
, 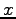 ,
, 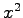 ,
, 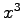 ,
,  ,
, 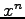 ,
, 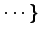 をもつ.
無限個の基底をもつので,
をもつ.
無限個の基底をもつので,
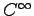 は無限次元のベクトル空間である.
は無限次元のベクトル空間である.
 |
全体の集合であるから, 基底として
問 3.111 (線形微分方程式の解集合)
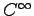 の部分空間
の部分空間
は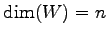 をみたす.
これを示せ.
をみたす.
これを示せ.
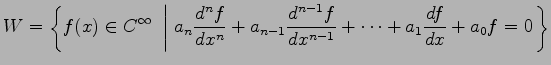 |
は
平成20年2月2日