3.23 演習問題 〜 1 次独立なベクトルの最大個数
問 3.92 (1 次独立なベクトルの最大個数)
次のベクトルの組の 1 次独立なベクトルの最大個数と
そのときの組合わせのひとつを示せ.
また,それ以外の 1 次従属なベクトルを
1 次独立なベクトルの 1 次結合で表わせ.
(1)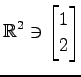 ,
,
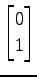 (2)
(2)
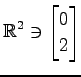 ,
,
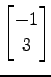 ,
,
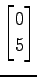 (3)
(3)
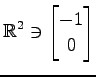 ,
,
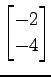 ,
,
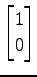 ,
,
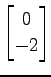
(4)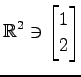 ,
,
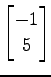 ,
,
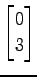 ,
,
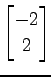 (5)
(5)
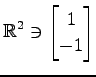 ,
,
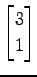 ,
,
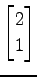 ,
,
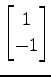 ,
,
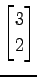 (6)
(6)
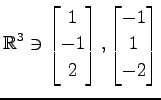
(7)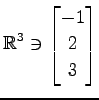 ,
,
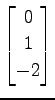 ,
,
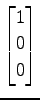 (8)
(8)
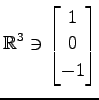 ,
,
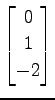 ,
,
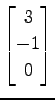 ,
,
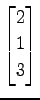
(9)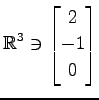 ,
,
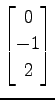 ,
,
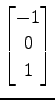 ,
,
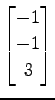 (10)
(10)
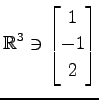 ,
,
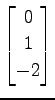 ,
,
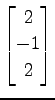 ,
,
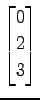 ,
,
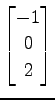
(11)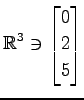 ,
,
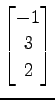 ,
,
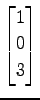 ,
,
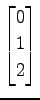 ,
,
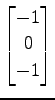 ,
,
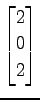 (12)
(12)
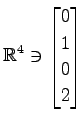 ,
,
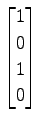 ,
,
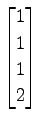
(13)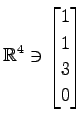 ,
,
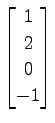 ,
,
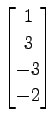 ,
,
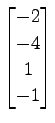 ,
,
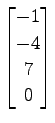 (14)
(14)
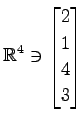 ,
,
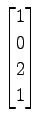 ,
,
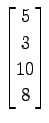 ,
,
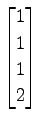 ,
,
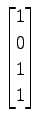
(15)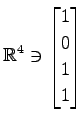 ,
,
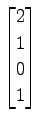 ,
,
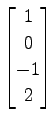 ,
,
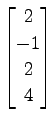 ,
,
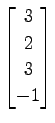 (16)
(16)
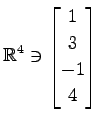 ,
,
 ,
,
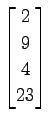
(17)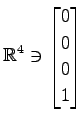 ,
,
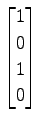 ,
,
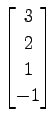 ,
,
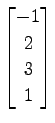 ,
,
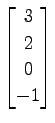 .
(18)
.
(18)
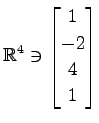 ,
,
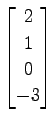 ,
,
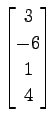
(19)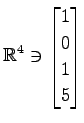 ,
,
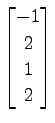 ,
,
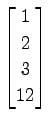 (20)
(20)
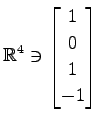 ,
,
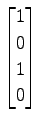 ,
,
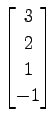 ,
,
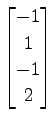 ,
,
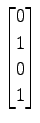 ,
,
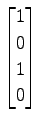
(21)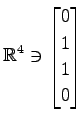 ,
,
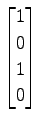 ,
,
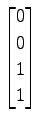 .
.
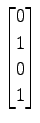 ,
,
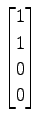 ,
,
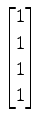 (22)
(22)
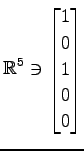 ,
,
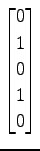 ,
,
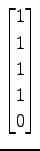
(23)![$ \mathbb{R}[x]_3\ni 1+x+3x^2$](img1202.png) ,
, 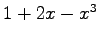 ,
,
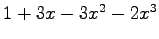 ,
,
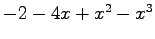 ,
,
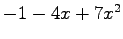
(24)![$ \mathbb{R}[x]_3\ni 1+2x$](img1207.png) ,
, 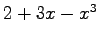 ,
,
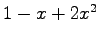 ,
, 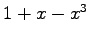 ,
, 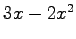
(25)![$ \mathbb{R}[x]_4\ni 1+x-x^2+2x^3+x^4$](img1212.png) ,
, 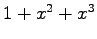 ,
,
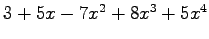 ,
,
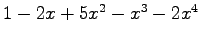 ,
,
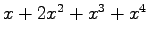
(1)
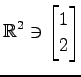 ,
,
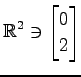 ,
,
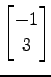 ,
,
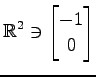 ,
,
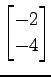 ,
,
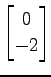
(4)
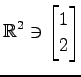 ,
,
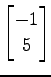 ,
,
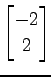 (5)
(5)
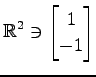 ,
,
 ,
,
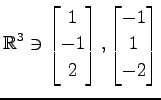
(7)
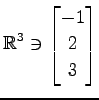 ,
,
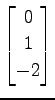 ,
,
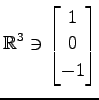 ,
,
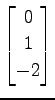 ,
,
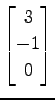 ,
,
(9)
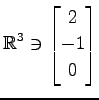 ,
,
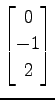 ,
,
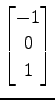 ,
,
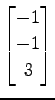 (10)
(10)
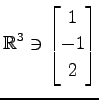 ,
,
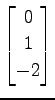 ,
,
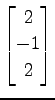 ,
,
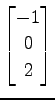
(11)
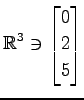 ,
,
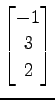 ,
,
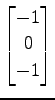 ,
,
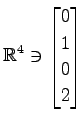 ,
,
(13)
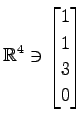 ,
,
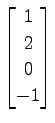 ,
,
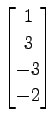 ,
,
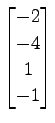 ,
,
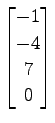 (14)
(14)
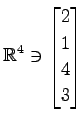 ,
,
(15)
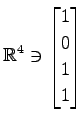 ,
,
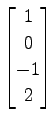 ,
,
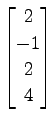 ,
,
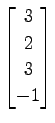 (16)
(16)
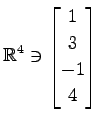 ,
,
 ,
,
(17)
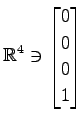 ,
,
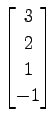 ,
,
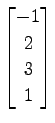 ,
,
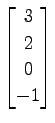 .
(18)
.
(18)
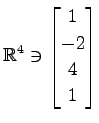 ,
,
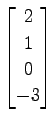 ,
,
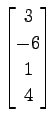
(19)
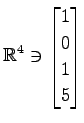 ,
,
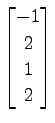 ,
,
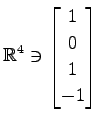 ,
,
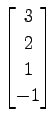 ,
,
 ,
,
(21)
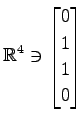 ,
,
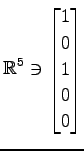 ,
,
(23)
(24)
(25)
問 3.93 (1 次独立なベクトルの最大個数)
次の行列の列ベクトルの 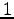 次独立なベクトルの最大個数を述べよ.
また,行ベクトルの
次独立なベクトルの最大個数を述べよ.
また,行ベクトルの 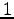 次独立なベクトルの最大個数を述べよ.
次独立なベクトルの最大個数を述べよ.
(1)
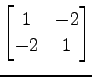 (2)
(2)
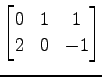 (3)
(3)
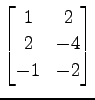 (4)
(4)
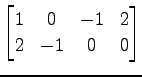
(5)
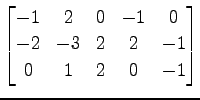 (6)
(6)
 (7)
(7)

平成20年2月2日