4.9 線形写像の階数と退化次数
定義 4.44 (階数,退化次数)
線形写像  の像
の像
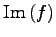 の次元を階数(rank)といい,
の次元を階数(rank)といい,
と表記する. また,核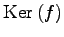 の次元を
退化次数(nullity)といい,
の次元を
退化次数(nullity)といい,
と表記する.
と表記する. また,核
と表記する.
定理 4.45 (退化次数,階数)
線形写像
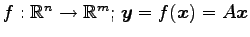 の階数は
の階数は
である.また, の退化次数は
の退化次数は
である.
である. これは方程式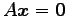 の解空間である.
方程式
の解空間である.
方程式
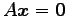 の
一般解の任意定数の個数
の
一般解の任意定数の個数
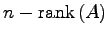 が
解空間の次元と等しいので,
が
解空間の次元と等しいので,
が成り立つ. 次に の像は定義より
の像は定義より
である.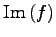 の任意の元は
の任意の元は
と表される. つまり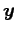 の集合はベクトル
の集合はベクトル
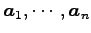 で
張られる部分空間
で
張られる部分空間
となる. 部分空間の基底の個数は 1 次独立なベクトルの最大個数となるから,
が成り立つ.
である.また,
である.
(証明)
まず ![]() の核は定義より
の核は定義より
である. これは方程式
が成り立つ. 次に
である.
 |
と表される. つまり
となる. 部分空間の基底の個数は 1 次独立なベクトルの最大個数となるから,
が成り立つ.
注意 4.46 (退化次数,階数)
線形写像
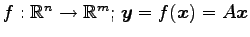 に対して
に対して
が成り立つことに注意する.
が成り立つことに注意する.
定理 4.47 (退化次数,階数)
線形写像 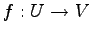 に関して
に関して
が成立する.
をみたすとする. このとき 1 次関係
に対して を作用させると
を作用させると
となる.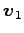 ,
,  ,
, 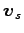 は
1 次独立なので
は
1 次独立なので
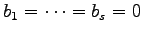 となる.
このとき
となる.
このとき
であり,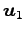 ,
,  ,
, 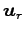 は
1 次独立であるか
は
1 次独立であるか
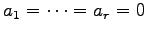 となる.
よって
となる.
よって
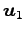 ,
,  ,
,
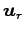 ,
,
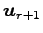 ,
,  ,
,
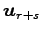 は
1 次独立である.
次に,
は
1 次独立である.
次に,
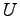 の任意のベクトル
の任意のベクトル 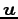 を
を  で写された
ベクトル
で写された
ベクトル
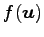 は
は 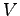 のベクトルであるから,
のベクトルであるから,
と書ける. これより
が成り立つ. ベクトル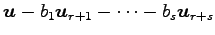 は
は
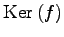 に含まれる.よって
に含まれる.よって
と書けるので,
を得る. ,
,
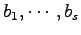 は任意であるから,
は任意であるから,
となる. 以上より,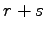 個のベクトル
個のベクトル
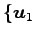 ,
,  ,
, 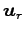 ,
,
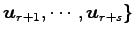 が
が
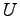 の基底となる,
よって
の基底となる,
よって
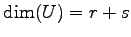 ,
,
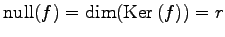 ,
,
 を得る.
を得る.
が成立する.
(証明)
![]() の基底を
の基底を
![]() ,
, ![]() ,
,
![]() とし,
とし,
![]() の基底を
の基底を
![]() ,
, ![]() ,
,
![]() とする.
また,
とする.
また,![]() のベクトル
のベクトル
![]() が
が
をみたすとする. このとき 1 次関係
に対して
となる.
であり,
と書ける. これより
が成り立つ. ベクトル
と書けるので,
を得る.
となる. 以上より,
例 4.48 (線形写像の像と核の具体例)
線形写像
の像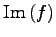 ,核
,核
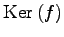 と
それらの次元である階数
と
それらの次元である階数
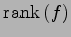 , 退化次数
, 退化次数
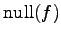 を求める.
を求める.
となる. このとき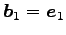 ,
,
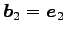 は
1 次独立であり,その他のベクトルは
は
1 次独立であり,その他のベクトルは
と表される. 同じ 1 次関係が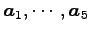 に対しても成り立つので,
に対しても成り立つので,
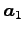 ,
, 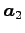 は 1 次独立であり,
その他のベクトルは
は 1 次独立であり,
その他のベクトルは
となる. また,方程式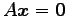 の解は
の解は
と表される.
となる.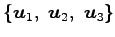 は 1 次独立であり,
は 1 次独立であり,
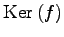 の基底となる.
よって退化次数は
の基底となる.
よって退化次数は
と得られる.
により定まる. (☆)を用いると
と表される.ここで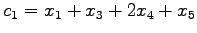 ,
,
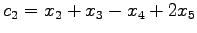 は任意の実数であるから,
は任意の実数であるから,
が成り立つ.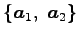 は 1 次独立であり,
は 1 次独立であり,
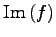 の基底となる.よって
の基底となる.よって
を得る.
であり,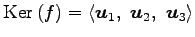 ,
,
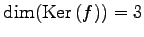 と表された.
この結果は
つまり,3 次元空間
と表された.
この結果は
つまり,3 次元空間
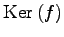 内のすべての点が
写像
内のすべての点が
写像  によりすべて一つの点
によりすべて一つの点
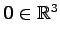 に写されることを意味する.
点は零次元の空間である.
よって,写像
に写されることを意味する.
点は零次元の空間である.
よって,写像  は次元を 3 次元退化させている.
それでは,
は次元を 3 次元退化させている.
それでは,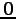 以外の点
以外の点
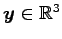 に
写される場合はどうであろうか.
つまり,
に
写される場合はどうであろうか.
つまり,
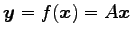 をみたす
をみたす
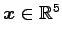 の集合を求める.
の集合を求める.
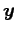 を
を
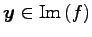 となるように選べば,
非同次方程式
となるように選べば,
非同次方程式
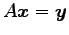 の一般解が存在する.
このとき,一般解は
の一般解が存在する.
このとき,一般解は
となる. ここで,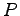 は
は 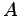 の簡約化行列とする.
の簡約化行列とする.
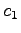 ,
, 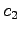 ,
, 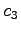 は任意の実数であるから,
方程式
は任意の実数であるから,
方程式
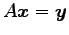 の解空間は 3 次元となる.
ただし,この解空間
の解空間は 3 次元となる.
ただし,この解空間
は原点を通らないのでベクトル空間ではない. 核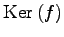 を
を 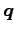 だけ平行移動した空間となる.
よって,写像
だけ平行移動した空間となる.
よって,写像  は
任意の
は
任意の
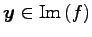 に対して
3 次元空間
に対して
3 次元空間
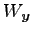 内のすべての点をひとつの点
内のすべての点をひとつの点 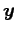 に写す写像である.
次元を 3 次元退化させている.
に写す写像である.
次元を 3 次元退化させている.
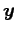 は
は
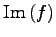 のベクトルであり,
のベクトルであり,
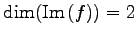 であるから,
1 次独立となるベクトルを二つ
であるから,
1 次独立となるベクトルを二つ 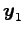 ,
, 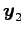 選べる.
このとき
選べる.
このとき
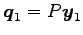 ,
,
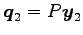 も
1 次独立となる.
も
1 次独立となる.
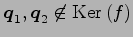 であり,
であり,
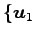 ,
,
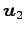 ,
,
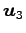 ,
,
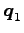 ,
,
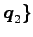 は
は
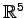 の基底となる.
よって,
の基底となる.
よって,
と表される. これより
が成立する.
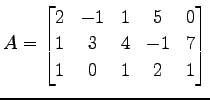 |
の像
まず ![]() を簡約化すると
を簡約化すると
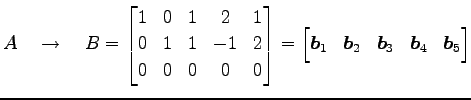 |
となる. このとき
と表される. 同じ 1 次関係が
となる. また,方程式
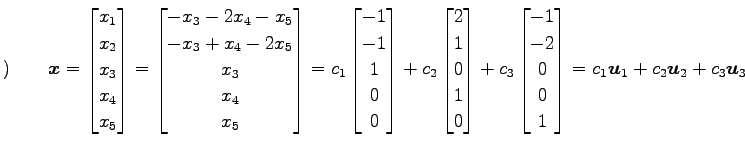 |
と表される.
![]() の核
の核
![]() は方程式
は方程式
![]() の
解(★)の集合であるから,
の
解(★)の集合であるから,
となる.
と得られる.
![]() の像
の像
![]() の元
の元 ![]() は
任意のベクトル
は
任意のベクトル
![]() に対して,
に対して,
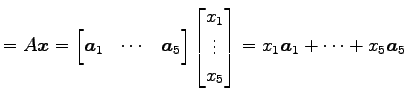 |
により定まる. (☆)を用いると
と表される.ここで
が成り立つ.
を得る.
以上より,
核
![]() は方程式
は方程式
![]() の解空間であるから,
核の任意のベクトルは一般解
の解空間であるから,
核の任意のベクトルは一般解
であり,
となる. ここで,
は原点を通らないのでベクトル空間ではない. 核
と表される. これより
が成立する.
平成20年2月2日