4.12 正則変換と逆変換
定義 4.54 (正則変換)
線形変換 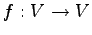 が上への 1 対 1 写像であるとき,
が上への 1 対 1 写像であるとき,
 を正則変換(regular mappping) という.
を正則変換(regular mappping) という.
注意 4.55 (逆変換)
上への 1 対 1 写像であれば逆変換 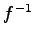 が存在する.
正則変換は逆変換が存在する線形変換である,と読み替えてもよい.
が存在する.
正則変換は逆変換が存在する線形変換である,と読み替えてもよい.
定理 4.56 (正則変換と正則行列)
線形写像  が正則変換であることと,
が正則変換であることと,
 の表現行列が正則行列であることとは必用十分な条件である.
の表現行列が正則行列であることとは必用十分な条件である.
が成り立つ. 恒等変換の表現行列は単位行列 であるから,
であるから,
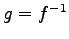 のとき
のとき
が成り立つ.よって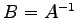 を得る.
を得る.
(証明)
(
![]() )
写像
)
写像 ![]() ,
, ![]() ,
, ![]() の表現行列を
の表現行列を ![]() ,
, ![]() ,
, ![]() とする.
このとき
とする.
このとき
が成り立つ. 恒等変換の表現行列は単位行列
が成り立つ.よって
注意 4.57 (逆変換と逆行列)
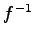 が存在することと,
が存在することと,
 の表現行列
の表現行列 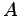 の逆行列
の逆行列 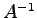 が存在することは等価である.
が存在することは等価である.
例 4.58 (正則変換の具体例)
線形写像
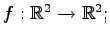
の表現行列とその行列式は
である.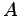 は正則行列であるから,
は正則行列であるから, は正則変換である.
は正則変換である.
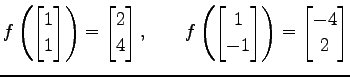 |
の表現行列とその行列式は
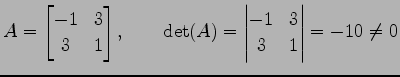 |
である.
例 4.59 (正則変換ではない具体例)
射影変換
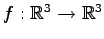 ;
;
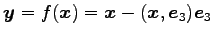 の
表現行列とその行列式は
の
表現行列とその行列式は
である. よって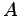 は正則でないので
は正則でないので  もまた正則ではない.
もまた正則ではない.
 |
である. よって
例えば点
![]() と点
と点
![]() を
射影変換
を
射影変換 ![]() で写すとどちらも点
で写すとどちらも点
![]() に写される.
他にも点
に写される.
他にも点
![]() を通り軸
を通り軸 ![]() に平行な直線上の点は全て
に平行な直線上の点は全て
![]() により点
により点
![]() に写される.
逆変換
に写される.
逆変換 ![]() を考えるとき点
を考えるとき点
![]() から戻され点は
直線上に無限に存在することになる.
よって
から戻され点は
直線上に無限に存在することになる.
よって ![]() は 1 対 1 写像ではない.
また,
は 1 対 1 写像ではない.
また,
![]() の任意の点は
の任意の点は ![]() により
全て
により
全て
![]() 平面上に写される.
平面上に写される.
![]() 平面は
平面は
![]() の部分空間であるので,
の部分空間であるので,
![]() は上への写像でもない.
は上への写像でもない.
注意 4.60 (核と正則変換)
線形変換 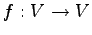 が
が
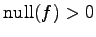 のとき,
のとき,
 は正則変換ではない.
なぜなら,
は正則変換ではない.
なぜなら,
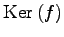 のすべての元は
のすべての元は 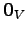 に写されるので,
に写されるので,
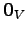 の逆元は存在しない.
よって,
の逆元は存在しない.
よって, は 1 対 1 の写像ではなく,正則変換はない.
は 1 対 1 の写像ではなく,正則変換はない.
平成20年2月2日