4.14 直交行列
定義 4.64 (直交行列)
行列
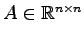 が
が
をみたすとき を
直交行列(orthogonal matrix)という.
を
直交行列(orthogonal matrix)という.
をみたすとき
定理 4.65 (直交行列の行列式)
直交行列の行列式は
である.
となるので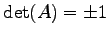 を得る.
を得る.
である.
(証明)
![]() より,両辺の行列式をとると
より,両辺の行列式をとると
となるので
定理 4.66 (直交行列の正則性)
直交行列は正則である.
(証明)
![]() であるから.
であるから.
定理 4.67 (直交行列の逆行列)
直交行列の逆行列は
であり,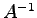 もまた直交行列である.
もまた直交行列である.
を得る.
であり,
(証明)
![]() は正則であるか
は正則であるか ![]() を
を
![]() に左から掛けると
に左から掛けると
を得る.
定理 4.68 (直交行列の積)
直交行列の積もまた直交行列である.
(証明)
![]() ,
, ![]() を直交行列として,
を直交行列として,
平成20年2月2日