4.19
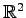 における回転
における回転
![]() 内での原点を中心とする角
内での原点を中心とする角 ![]() の回転移動を考える.
点
の回転移動を考える.
点 ![]() から点
から点 ![]() への変換を
への変換を ![]() とする.
このとき,
標準基底
とする.
このとき,
標準基底
![]() は
は
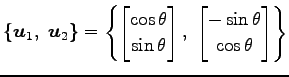 |
へ写されるので,
が成り立つ. よって
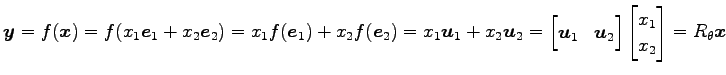 |
となる. ただし,
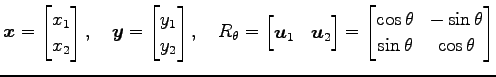 |
とおく. 以上より, 原点を中心として角
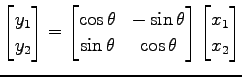 |
と表される. この逆変換は
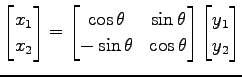 |
と表される.
問 4.84 (回転行列)
次の関係式が成り立つことを示せ.
注意 4.85 (回転行列と鏡映変換)
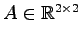 のすべての直交行列
のすべての直交行列
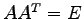 は
回転変換行列
は
回転変換行列
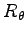 と
と
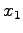 軸に対する鏡映変換行列
軸に対する鏡映変換行列
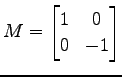 の積の組合わせで表される.
の積の組合わせで表される.
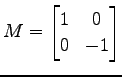 の積の組合わせで表される.
の積の組合わせで表される.
平成20年2月2日