4.20
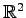 における鏡映変換
における鏡映変換
定義 4.86 (鏡映変換)
typing...
例 4.87 (鏡映変換の具体例)
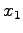 軸に関する鏡映変換を考える.
任意の点
軸に関する鏡映変換を考える.
任意の点 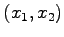 は
は
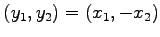 に写されるので,
鏡映変換は
に写されるので,
鏡映変換は
と表される.表現行列は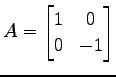 である.
である.
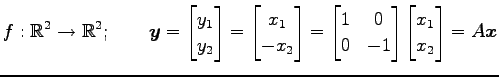 |
と表される.表現行列は
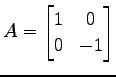 である.
である.
例 4.88 (鏡映変換の具体例)
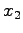 軸に関する鏡映変換を考える.
任意の点
軸に関する鏡映変換を考える.
任意の点 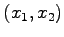 は
は
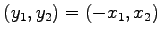 に写されるので,
鏡映変換は
に写されるので,
鏡映変換は
と表される.表現行列は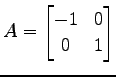 である.
である.
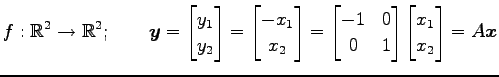 |
と表される.表現行列は
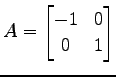 である.
である.
例 4.89 (鏡映変換の具体例)
直線 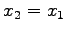 に関する鏡映変換を考える.
この直線は
に関する鏡映変換を考える.
この直線は 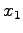 軸に対して
軸に対して
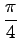 の角度であるから,
の角度であるから,
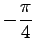 回転するとこの直線は
回転するとこの直線は 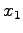 軸と重なる.
このとき鏡映変換は
軸と重なる.
このとき鏡映変換は 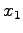 軸に対する鏡映変換とみなせる.
鏡映変換された点を
軸に対する鏡映変換とみなせる.
鏡映変換された点を
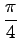 回転すると
直線
回転すると
直線 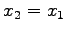 に関する鏡映変換とみせる.
よって,合成変換となるので表現行列は
に関する鏡映変換とみせる.
よって,合成変換となるので表現行列は
となる. 直線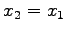 に関する鏡映変換は
に関する鏡映変換は
である. 表現行列は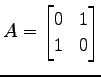 である.
任意の点
である.
任意の点 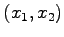 は
は 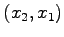 に写される.
に写される.
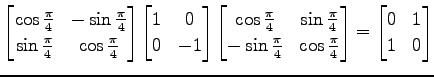 |
となる. 直線
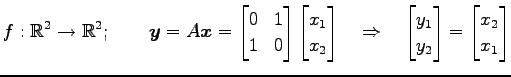 |
である. 表現行列は
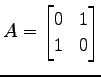 である.
任意の点
である.
任意の点
注意 4.90 (鏡映変換行列と直交行列)
鏡映変換の表現行列は直交行列となる.
平成20年2月2日