5.4 三角関数のテイラー級数
例 5.5 (三角関数のテイラー級数)
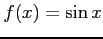 とおく.
導関数を計算すると
とおく.
導関数を計算すると
である.一般的に書くと
である.点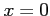 における微分係数は
における微分係数は
と求まる. これを用いてテーラー級数を求めると
を得る. 収束半径を求める.
とおくと
が得られる.
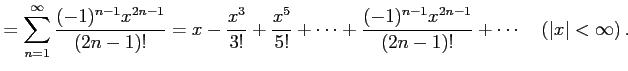 |
||
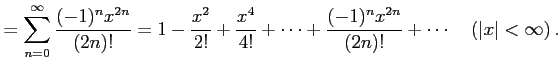 |
(導出)
である.一般的に書くと
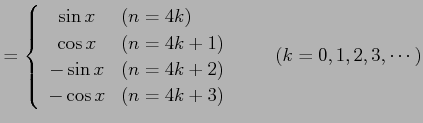 |
である.点
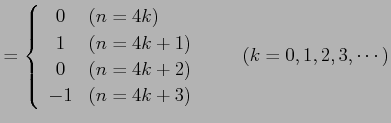 |
と求まる. これを用いてテーラー級数を求めると
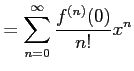 |
||
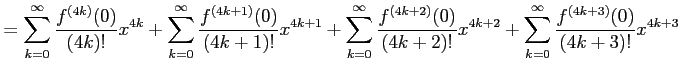 |
||
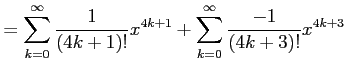 |
||
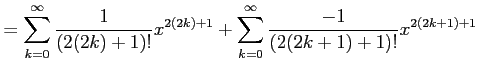 |
||
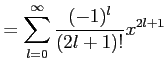 |
||
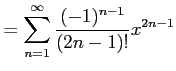 |
を得る. 収束半径を求める.
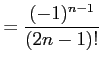 |
とおくと
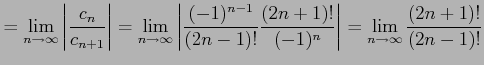 |
||
が得られる.
例 5.6 (三角関数のテイラー級数)
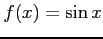 の点
の点
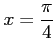 まわりでのテイラー級数を求める.
まわりでのテイラー級数を求める.
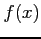 の高階導関数は前述の問題で求めているので,
の高階導関数は前述の問題で求めているので,
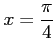 における高階微係数を求めると,
における高階微係数を求めると,
となる.よって,テイラー級数は
と得られる.
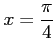 まわりでのテイラー級数を求める.
まわりでのテイラー級数を求める.
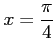 における高階微係数を求めると,
における高階微係数を求めると,
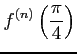 |
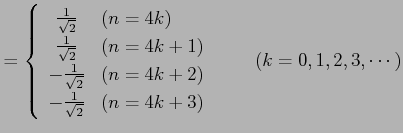 |
となる.よって,テイラー級数は
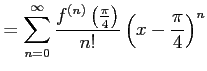 |
||
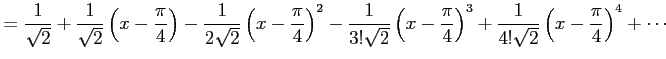 |
||
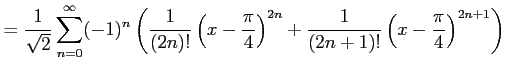 |
と得られる.
平成21年6月1日