3.18 演習 〜 微分
問 3.38 (微分係数)
次の定義を述べよ.
(1) 点 ![]() における関数
における関数 ![]() の微分係数
の微分係数 ![]() .
(2) 関数
.
(2) 関数 ![]() の導関数
の導関数 ![]() .
.
問 3.39 (微分の性質)
次を証明せよ.ただし,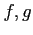 は微分可能とする.
は微分可能とする.
(1)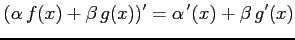 (2)
(2)
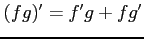
(1)
問 3.40 (微分可能)
次の関数について(i) 関数 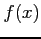 のグラフを描け.
(ii)
のグラフを描け.
(ii) 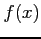 の微分不可能な点を述べよ.
また,この点における右微分係数,左微分係数を求めよ.
(iii) 微分可能な範囲で導関数
の微分不可能な点を述べよ.
また,この点における右微分係数,左微分係数を求めよ.
(iii) 微分可能な範囲で導関数 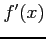 を求めよ.
(iv)
を求めよ.
(iv) 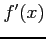 のグラフを描け.
のグラフを描け.
(1)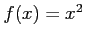 (2)
(2) 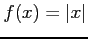 (3)
(3)
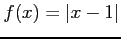 (4)
(4)
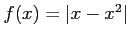
(5)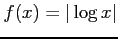
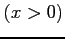
(1)
(5)
問 3.41 (初等関数の導関数)
次の関数の導関数を書け.
(1)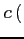 $c$:定数
$c$:定数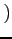 (2)
(2)
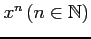 (3)
(3)
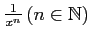 (4)
(4)
![$ \sqrt[n]{x}\,(n\in\mathbb{N})$](img1201.png) (5)
(5)
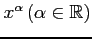
(6)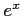 (7)
(7)
 (8)
(8) 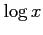 (9)
(9) 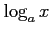 (10)
(10) 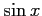 (11)
(11) 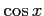 (12)
(12) 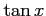
(13)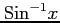 (14)
(14)
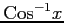 (15)
(15)
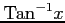 (16)
(16) 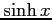 (17)
(17) 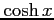 (18)
(18) 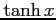
(19)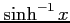 (20)
(20)
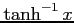 (21)
(21)
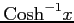
(1)
(6)
(13)
(19)
問 3.42 (導関数の導出)
次を証明せよ.ただし,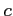 は定数,
は定数,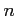 は自然数とする.
は自然数とする.
(1) (2)
(2)
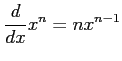 (3)
(3)
 (4)
(4)
![$ \displaystyle{\frac{d}{dx}\sqrt[n]{x}=\frac{\sqrt[n]{x}}{n x}}$](img1208.png)
(5)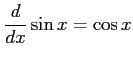 (6)
(6)
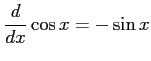 (7)
(7)
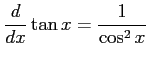
(8)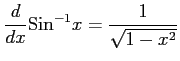 (9)
(9)
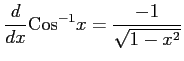 (10)
(10)
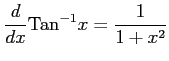
(11)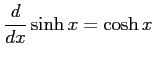 (12)
(12)
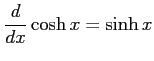 (13)
(13)
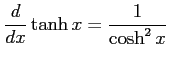
(14) (15)
(15)
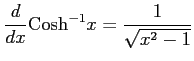 (16)
(16)
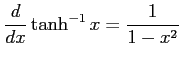
(17)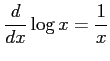 (18)
(18)
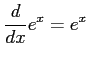 (19)
(19)
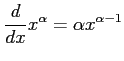 (
(
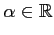 )
)
(1)
 (2)
(2)
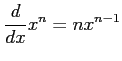 (3)
(3)
 (4)
(4)
![$ \displaystyle{\frac{d}{dx}\sqrt[n]{x}=\frac{\sqrt[n]{x}}{n x}}$](img1208.png)
(5)
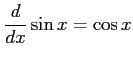 (6)
(6)
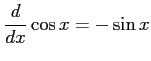 (7)
(7)
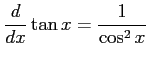
(8)
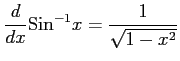 (9)
(9)
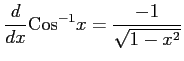 (10)
(10)
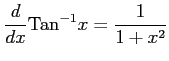
(11)
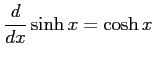 (12)
(12)
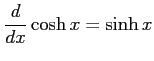 (13)
(13)
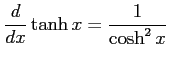
(14)
 (15)
(15)
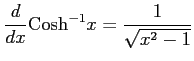 (16)
(16)
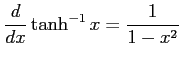
(17)
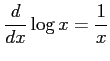 (18)
(18)
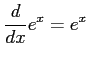 (19)
(19)
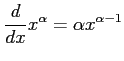 (
(
問 3.43 (微分の計算)
次の関数の導関数を求めよ.
(1) (2)
(2)
 (3)
(3)
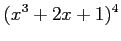 (4)
(4)
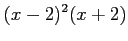
(5)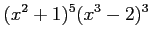 (6)
(6)
 (7)
(7)
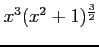 (8)
(8)
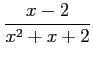 (9)
(9)
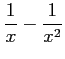
(10)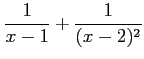 (11)
(11)
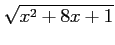 (12)
(12)
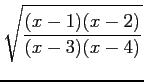 (13)
(13)
![$ \displaystyle{\sqrt[\leftroot{2} \uproot{2} 3]{\frac{x+2}{x^2+1}}}$](img1237.png)
(14)![$ \displaystyle{\sqrt[\leftroot{2} \uproot{2} 3]{\frac{x^2+1}{(x-1)^2}}}$](img1238.png) (15)
(15)
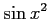 (16)
(16)
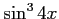 (17)
(17)
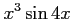 (18)
(18)
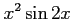 (19)
(19)
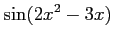
(20)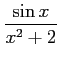 (21)
(21)
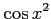 (22)
(22)
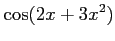 (23)
(23)
 (24)
(24)
 (25)
(25)
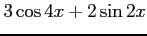
(26)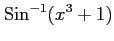 (27)
(27)
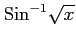 (28)
(28)
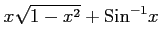 (29)
(29)
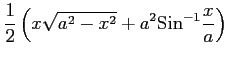
(30)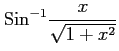 (31)
(31)
 (32)
(32)
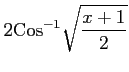 (33)
(33)
 (34)
(34)
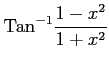
(35)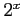 (36)
(36)
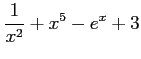 (37)
(37)
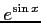 (38)
(38)
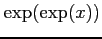 (39)
(39)

(40)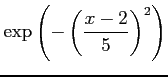 (41)
(41)
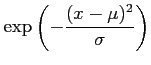 (42)
(42)
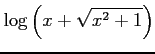 (43)
(43)

(44)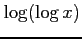 (45)
(45)
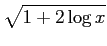 (46)
(46)
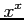
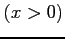 (47)
(47)
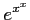 (48)
(48)
 (49)
(49)
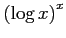
(1)
(5)
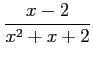 (9)
(9)
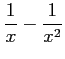
(10)
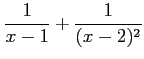 (11)
(11)
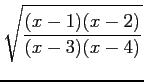 (13)
(13)
![$ \displaystyle{\sqrt[\leftroot{2} \uproot{2} 3]{\frac{x+2}{x^2+1}}}$](img1237.png)
(14)
![$ \displaystyle{\sqrt[\leftroot{2} \uproot{2} 3]{\frac{x^2+1}{(x-1)^2}}}$](img1238.png) (15)
(15)
(20)
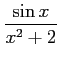 (21)
(21)
(26)
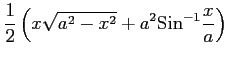
(30)
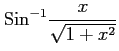 (31)
(31)
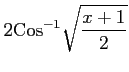 (33)
(33)
 (34)
(34)
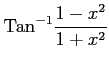
(35)
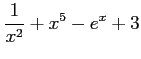 (37)
(37)
(40)
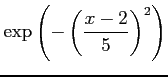 (41)
(41)
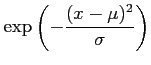 (42)
(42)
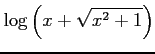 (43)
(43)

(44)
問 3.44 (接線)
次の関数について
(i) 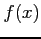 のグラフを書け.
(ii)
のグラフを書け.
(ii) 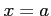 における接線の方程式を求めよ.
(iii) 接線のグラフを書け.
における接線の方程式を求めよ.
(iii) 接線のグラフを書け.
(1) ,
, 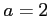 (2)
(2) 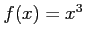 ,
, 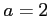
(3) ,
, 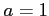 ,
, 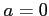 ,
,
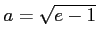 (4)
(4)
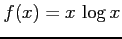 ,
, 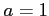 ,
, 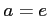
(5) ,
,
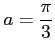 (6)
(6)
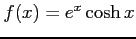 ,
, 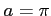
(7) ,
,
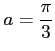 (8)
(8)
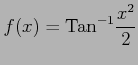 ,
,
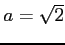
(1)
(3)
(5)
 ,
,
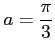 (6)
(6)
(7)
 ,
,
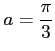 (8)
(8)
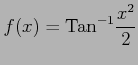 ,
,
問 3.45 (接線)
次の曲線 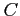 の点
の点 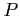 における接線の方程式を求めよ.
における接線の方程式を求めよ.
(1)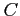 :
: 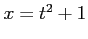 ,
, 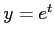 ;
; 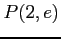 (2)
(2) 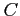 :
:
 ,
,
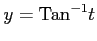 ;
;
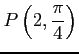
(3) :
:
 ,
,
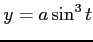 ;
;
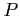 は
は
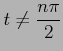 (
(
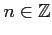 ) の点
) の点
(1)
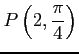
(3)
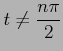 (
(
問 3.46 (なめらかさ)
次の関数 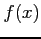 の導関数
の導関数 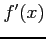 は連続関数であるか述べよ.
は連続関数であるか述べよ.
(1)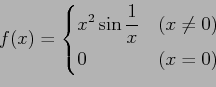 (2)
(2)
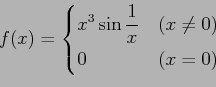
(1)
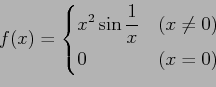 (2)
(2)
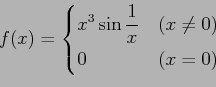
問 3.47 (増減)
次の関数の増減,極値,最大値,最小値を調べグラフを描け.
(1)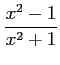 (2)
(2)
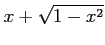 (3)
(3)
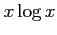 (4)
(4)
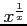
(1)
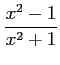 (2)
(2)
問 3.48 (不等式)
次の不等式を示せ.
(1)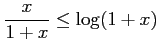 (
(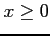 )
(2)
)
(2)
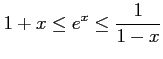 (
(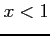 )
)
(3)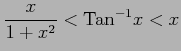 (
(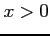 )
(4)
)
(4)
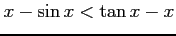
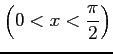
(1)
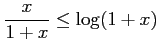 (
(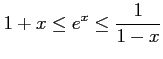 (
((3)
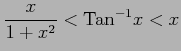 (
(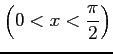
平成21年6月1日