2.17 点の直線への正射影
定義 2.39 (点の直線への正射影)
点  から直線
から直線 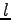 に垂線を下ろした足
に垂線を下ろした足 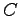 を
正射影という.
点
を
正射影という.
点  から点
から点 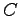 への変換を射影変換という.
への変換を射影変換という.
例 2.40 (正射影の具体例)
点 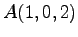 ,
, 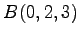 ,
,
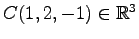 を考える.
点
を考える.
点 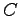 から直線
から直線 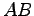 へ垂線を下ろした正射影を
へ垂線を下ろした正射影を 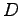 とする.
とする.
より
である.よって
となるので,
を得る.
![]() ,
,
![]() ,
,
![]() とおく.
このとき
とおく.
このとき
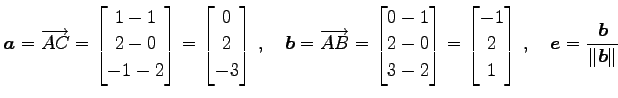 |
(78) |
より
 |
(79) |
である.よって
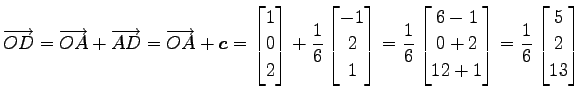 |
(80) |
となるので,
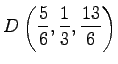 |
を得る.
平成20年4月22日