2.12 全微分可能性
定義 2.61 (全微分可能)
関数 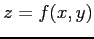 において,
点
において,
点  から点
から点
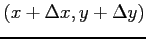 への
増分
への
増分
に対して
をみたす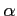 ,
, 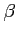 が存在するとき,
関数
が存在するとき,
関数 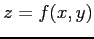 は
全微分可能(total differentiable)であるという.
このとき,
は
全微分可能(total differentiable)であるという.
このとき,
と表記し,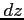 を
を 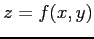 の全微分
または単に微分という.
の全微分
または単に微分という.
に対して
をみたす
と表記し,
例 2.62 (微分可能)
関数
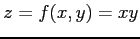 は全微分可能であるか考える.
まず,増分は
は全微分可能であるか考える.
まず,増分は
である.この増分が
の形をみたすと仮定する. このとき式変形すると
となる.ここで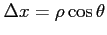 ,
,
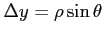 とおき,
とおき,
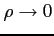 の極限をとると,
の極限をとると,
を得る.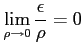 となるためには
となるためには
とおく. よって,
が成り立つ. 関数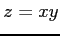 は全微分可能である.
また,
は全微分可能である.
また,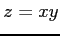 の全微分は
の全微分は
となる.
である.この増分が
の形をみたすと仮定する. このとき式変形すると
 |
となる.ここで
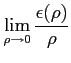 |
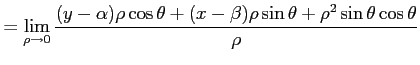 |
|
を得る.
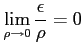 となるためには
となるためには
とおく. よって,
が成り立つ. 関数
となる.
例 2.63 (微分可能)
関数
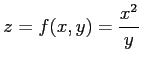 は全微分可能であるか考える.
まず,増分は
は全微分可能であるか考える.
まず,増分は
である.この増分が
の形をみたすと仮定する. このとき式変形すると
となる.ここで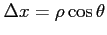 ,
,
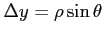 とおき,
とおき,
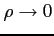 の極限をとると,
の極限をとると,
を得る.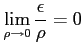 となるためには
となるためには
とおく. よって,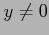 のとき
のとき
が成り立つ. 関数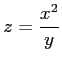 は
は 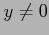 のとき全微分可能である.
また,
のとき全微分可能である.
また,
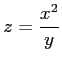 の全微分は
の全微分は
となる.
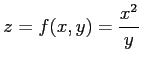 は全微分可能であるか考える.
まず,増分は
は全微分可能であるか考える.
まず,増分は
 |
||
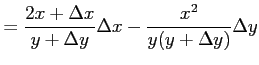 |
である.この増分が
の形をみたすと仮定する. このとき式変形すると
 |
となる.ここで
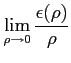 |
 |
|
 |
を得る.
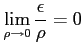 となるためには
となるためには
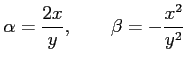 |
とおく. よって,
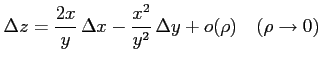 |
が成り立つ. 関数
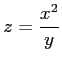 は
は 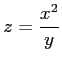 の全微分は
の全微分は
 |
となる.
例 2.64 (微分可能)
関数
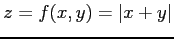 が原点で全微分可能であるか考える.
まず,原点における増分は
が原点で全微分可能であるか考える.
まず,原点における増分は
である.この増分が
の形をみたすと仮定する. このとき式変形すると
となる.ここで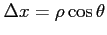 ,
,
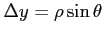 とおくと,
とおくと,
となる. 極限をとると
となる. これが 0 となる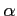 ,
, 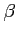 は
は
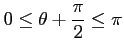 のとき
のとき
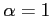 ,
, 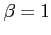 であり,
であり,
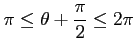 のとき
のとき
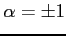 ,
,
 (復号同順)である.
よって,
極限の取り方によらず
(復号同順)である.
よって,
極限の取り方によらず
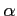 ,
, 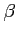 は一意に定まらないので,
は一意に定まらないので,
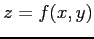 は原点で全微分不可能である.
は原点で全微分不可能である.
である.この増分が
の形をみたすと仮定する. このとき式変形すると
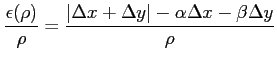 |
となる.ここで
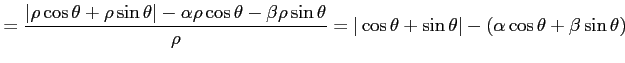 |
||
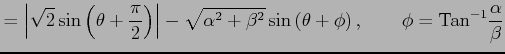 |
となる. 極限をとると
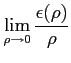 |
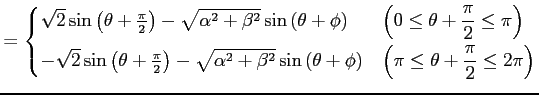 |
となる. これが 0 となる
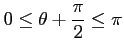 のとき
のとき
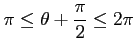 のとき
のとき
平成21年12月2日