2.13 多変数関数の全微分
定義 2.65 (全微分)
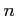 変数関数
変数関数
 において,
において,
をみたす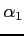 ,
,  ,
, 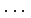 ,
,  が
存在するとき,
が
存在するとき,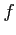 は全微分可能であるといい,
は全微分可能であるといい,
と表記する.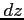 を
を  の全微分または微分という.
の全微分または微分という.
をみたす
と表記する.
平成21年12月2日
2.13 多変数関数の全微分
定義 2.65 (全微分)変数関数
において,
をみたす,
,
,
が 存在するとき,
は全微分可能であるといい,
と表記する.を
の全微分または微分という.
平成21年12月2日