2.17 演習問題 〜 ランダウの記号,全微分
問 2.75 (ランダウの記号)
次の式をみたす 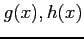 を書け.
を書け.
(1)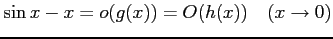 (2)
(2)
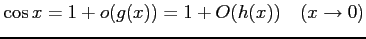
(3)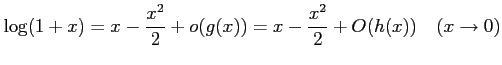
(4)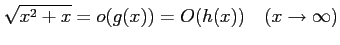
(1)
(3)
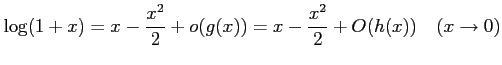
(4)
問 2.76 (ランダウの記号)
次の評価式の
 をうめて評価式を完成せよ.
をうめて評価式を完成せよ.
(1) (2)
(2)

(3)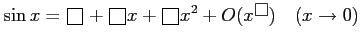 (4)
(4)
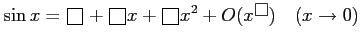
(5)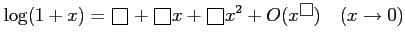
(6)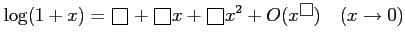
(7)
(8)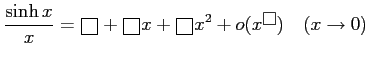
(9)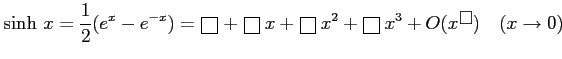
(1)
(3)
(5)
(6)
(7)
(8)
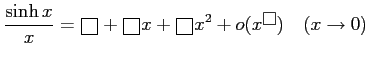
(9)
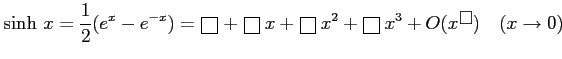
問 2.77 (全微分)
次の関数が全微分可能であるか議論せよ.
(1)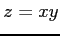 (2)
(2) 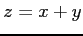 (3)
(3)
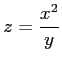 (4)
(4)
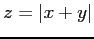
(ヒント)次の手順(i)-(v)で議論する. (i) 点 から点
から点
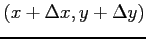 への
増分
への
増分  を求める.
(ii)
を求める.
(ii)
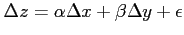 ,
,
 とおき,
とおき,
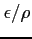 を求める.
(iii)
を求める.
(iii)
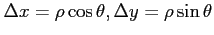 とおき,
極限
とおき,
極限
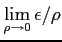 を求める.
(iv)
を求める.
(iv)
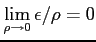 を
みたす有限な
を
みたす有限な
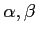 を決定する.
(v)
を決定する.
(v)
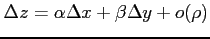 (
(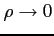 )
をみたす有限な
)
をみたす有限な
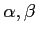 が一意に存在することを示す.
が一意に存在することを示す.
(1)
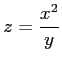 (4)
(4)
(ヒント)次の手順(i)-(v)で議論する. (i) 点
問 2.78 (全微分)
次の関数の全微分を求めよ.
(1) (2)
(2)
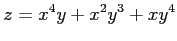 (3)
(3)
 (4)
(4)
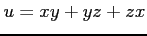
(5)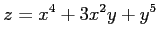 (6)
(6)
 (7)
(7)

(8)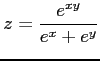 (9)
(9)
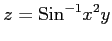 (10)
(10)

(1)
 (4)
(4)
(5)
(8)
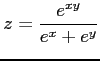 (9)
(9)

問 2.79 (全部分可能性と連続性)
次を示せ.
(1) 関数 が全微分可能なとき,
が全微分可能なとき,
 は偏微分可能である.
は偏微分可能である.
(2) 関数 が全微分可能なとき,
が全微分可能なとき,
 は連続である.
は連続である.
(1) 関数
(2) 関数
問 2.80 (2 変数関数の微分)
関数
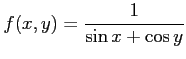 に対して,次の問に答えよ.
に対して,次の問に答えよ.
(1) 偏導関数 ,
,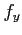 を求めよ.
(2) 偏微係数
を求めよ.
(2) 偏微係数  ,
, を求めよ.
を求めよ.
(3) 全微分 を求めよ.
(4) 原点において関数
を求めよ.
(4) 原点において関数  は連続であるか示せ.
は連続であるか示せ.
(5) 関数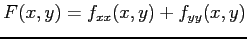 を求めよ.
を求めよ.
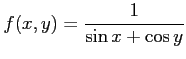 に対して,次の問に答えよ.
に対して,次の問に答えよ.
(1) 偏導関数
(3) 全微分
(5) 関数
平成21年12月2日