2.28 ヤコビアン

定義 2.115 (ヤコビアン)   座標変換 $(x_1,\cdots,x_n)\mapsto(u_1,\cdots,u_n)$ に対して， 行列式

$$\frac{\partial(x_1,x_2,\cdots,x_n)} {\partial(u_1,u_2,\cdots,u_n)... ...l x_n}{\partial u_2} & \cdots & \frac{\partial x_n}{\partial u_n} \end{bmatrix}$$

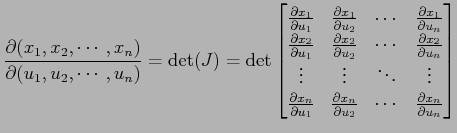をこの座標変換のヤコビアン（Jacobian） またはヤコビの行列式（Jacobi determinant）という．

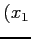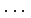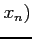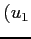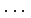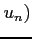注意 2.116 (座標変換)   ヤコビアンが非零となるときのみ， 座標 $(x_1$, $\cdots$, $x_n)$ と 座標 $(u_1$, $\cdots$, $u_n)$ とが 1 対 1 に対応する．

平成21年12月2日