2.33 演習問題 〜 偏微分作用素,座標変換
例 2.139 (偏微分作用素)
偏微分作用素
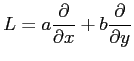 に対して,次が成り立つことを示せ.
ただし,
に対して,次が成り立つことを示せ.
ただし,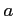 ,
, 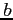 は定数とする.
は定数とする.
(1)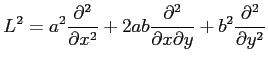 (2)
(2)
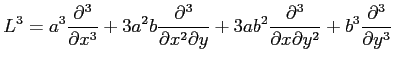
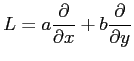 に対して,次が成り立つことを示せ.
ただし,
に対して,次が成り立つことを示せ.
ただし,(1)
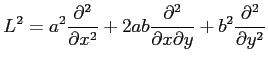 (2)
(2)
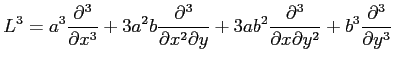
例 2.140 (偏微分作用素)
偏微分作用素
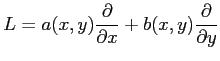 に対して,次が成り立つことを示せ.
ただし,
に対して,次が成り立つことを示せ.
ただし,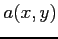 ,
, 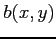 は関数とする.
は関数とする.
(1)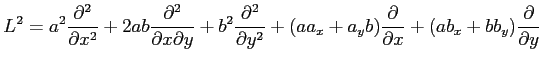
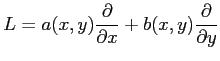 に対して,次が成り立つことを示せ.
ただし,
に対して,次が成り立つことを示せ.
ただし,(1)
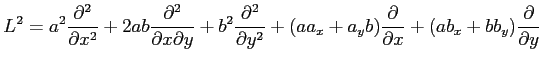
例 2.141 (ライプニッツ則)
1 変数関数 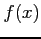 ,
, 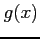 の積
の積 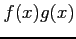 の微分が
の微分が
と書けることを用いて,次を求めよ.
(1)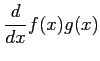 (2)
(2)
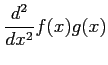 (3)
(3)
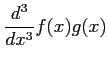 (4)
(4)
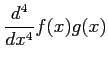 (5)
(5)
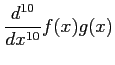
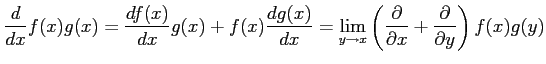 |
と書けることを用いて,次を求めよ.
(1)
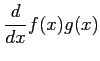 (2)
(2)
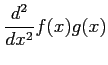 (3)
(3)
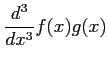 (4)
(4)
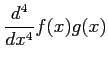 (5)
(5)
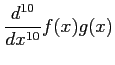
問 2.142 (座標変換)
座標変換
(i)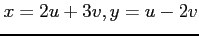 (ii)
(ii)
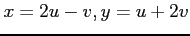 (iii)
(iii)
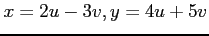
(iv)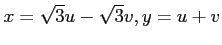 (v)
(v)
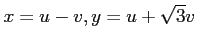
それぞれにおいて, 次を座標変換をせよ.
(1) ,
,
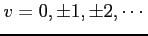 をみたす
をみたす  の軌跡をそれぞれ書け.
(2)
の軌跡をそれぞれ書け.
(2)
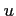 軸(
軸(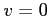 の直線)と
の直線)と 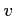 軸(
軸(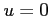 の直線)の
方向ベクトルを求めよ.
(3)
の直線)の
方向ベクトルを求めよ.
(3)
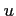 軸と
軸と 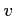 軸のなす角度を求めよ.
(4)
軸のなす角度を求めよ.
(4)
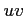 座標で
座標で
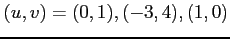 となる
点の
となる
点の 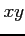 座標における座標
座標における座標  を求めよ.
(5)
を求めよ.
(5)
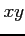 座標で
座標で
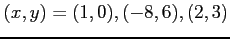 となる点の
となる点の 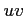 座標における座標
座標における座標 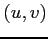 を求めよ.
(6)
直線
を求めよ.
(6)
直線 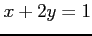 を座標
を座標 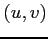 で表せ.
(7)
曲線
で表せ.
(7)
曲線  を座標
を座標 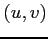 で表せ.
で表せ.
(8) ヤコビアン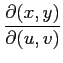 を求めよ.
(9)
を求めよ.
(9)  ,
, 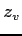 (10)
(10) 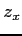 ,
, 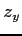 (11)
(11)
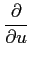 ,
,
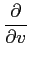 (12)
(12)
 ,
,

(13)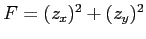 (14)
(14)
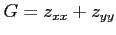 (15)
(15)
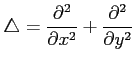 (16)
(16) 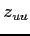 ,
,
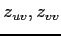
(i)
(iv)
それぞれにおいて, 次を座標変換をせよ.
(1)
(8) ヤコビアン
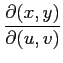 を求めよ.
(9)
を求めよ.
(9) (13)
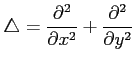 (16)
(16)
問 2.143 (直交座標と斜交座標)
標準基底
 ,
,
 から
基底
から
基底
![$ \vec{e}_u=\begin{bmatrix}\alpha \\ [-.5ex] \beta \end{bmatrix}$](img1158.png) ,
,
![$ \vec{e}_v=\begin{bmatrix}\gamma \\ [-.5ex] \delta \end{bmatrix}$](img1159.png) への座標変換
への座標変換
 ,
,
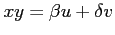 に関して次の問に答えよ.
に関して次の問に答えよ.
(1)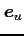 と
と 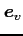 とが直交する
とが直交する
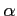 ,
, 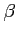 ,
, 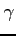 ,
, 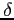 の条件を求めよ.
(2)
の条件を求めよ.
(2)
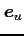 ,
, 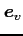 が単位ベクトルとなる
が単位ベクトルとなる
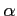 ,
, 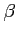 ,
, 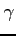 ,
, 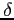 の条件を求めよ.
(3)
の条件を求めよ.
(3)
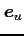 ,
, 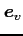 が正規直交基底となる
が正規直交基底となる
 ,
,  ,
, 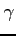 ,
, 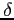 の条件を求めよ.
(4)
の条件を求めよ.
(4)
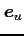 ,
, 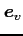 が正規直交基底となるとき,
基底の変換行列
が正規直交基底となるとき,
基底の変換行列
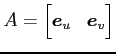 は直交行列となる
ことを示せ.
(ヒント:
は直交行列となる
ことを示せ.
(ヒント: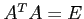 を示す.)
(5)
基底
を示す.)
(5)
基底 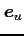 ,
, 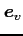 が
正規直交基底であるとき,
関数
が
正規直交基底であるとき,
関数
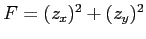 は
斜交座標
は
斜交座標 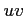 において,
において,
 と表されることを示せ.
(6)
基底
と表されることを示せ.
(6)
基底 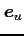 ,
, 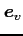 が
正規直交基底であるとき,
ラプラシアン
が
正規直交基底であるとき,
ラプラシアン
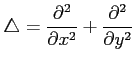 は斜交座標
は斜交座標 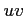 において,
において,
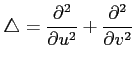 となることを示せ.
となることを示せ.
![$ \vec{e}_u=\begin{bmatrix}\alpha \\ [-.5ex] \beta \end{bmatrix}$](img1158.png) ,
,
![$ \vec{e}_v=\begin{bmatrix}\gamma \\ [-.5ex] \delta \end{bmatrix}$](img1159.png) への座標変換
への座標変換
(1)
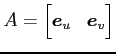 は直交行列となる
ことを示せ.
(ヒント:
は直交行列となる
ことを示せ.
(ヒント: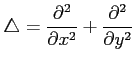 は斜交座標
は斜交座標 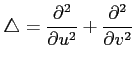 となることを示せ.
となることを示せ.
問 2.144 (座標変換)
座標変換
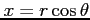 ,
,
 により,
次を座標変換せよ.
により,
次を座標変換せよ.
(1)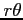 座標で
座標で
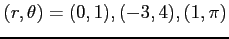 となる
点の
となる
点の 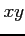 座標における座標
座標における座標  を求めよ.
を求めよ.
(2)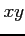 座標で
座標で
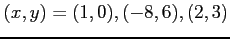 となる点の
となる点の 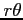 座標における座標
座標における座標
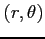 を求めよ.
を求めよ.
(3) ヤコビアン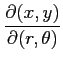 を求めよ.
(4)
を求めよ.
(4)
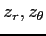 (5)
(5) 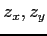 (6)
(6)
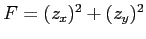
(7)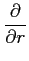 ,
,
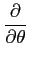 (8)
(8)
 ,
,
 (9)
(9)
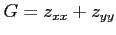 (10)
(10)
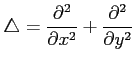 (11)
(11)
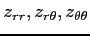
(1)
(2)
(3) ヤコビアン
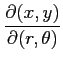 を求めよ.
(4)
を求めよ.
(4)
(7)
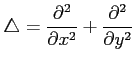 (11)
(11)
問 2.145 (3 次元の極座標)
3 次元の極座標変換
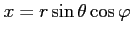 ,
,
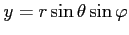 ,
,
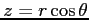 において次が成り立つことを示せ.
において次が成り立つことを示せ.
(1)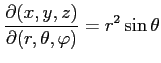 (2)
(2)
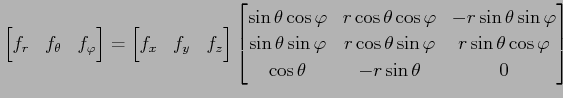
(3)
(4)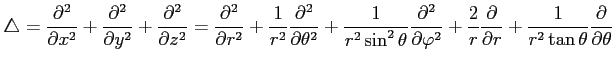
(1)
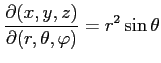 (2)
(2)
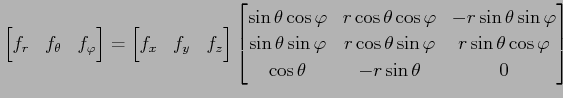
(3)

(4)
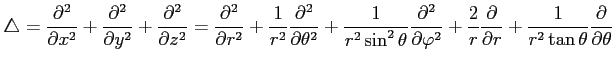
問 2.146 (調和関数と極座標)
次の関数にラプラシアン  を作用させた関数
を作用させた関数
 を
極座標に変換してから求めよ.
を
極座標に変換してから求めよ.
(1)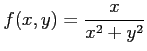 (2)
(2)
 (3)
(3)
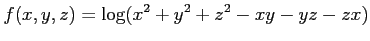
(1)
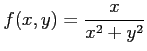 (2)
(2)
 (3)
(3)
問 2.147 (座標変換)
次の座標変換のヤコビアンを求めよ.
(1)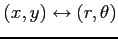 :
:
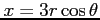 ,
,
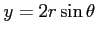 (2)
(2)
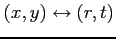 :
:
 ,
,
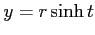
(3)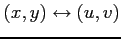 :
:
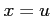 ,
, 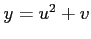 (4)
(4)
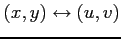 :
:
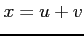 ,
, 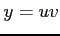
(5)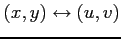 :
:
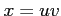 ,
, 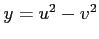
(6)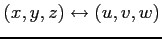 :
:
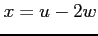 ,
, 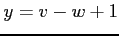 ,
, 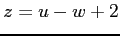
(1)
(3)
(5)
(6)
平成21年12月2日