2.42 接平面
注意 2.183 (曲面の法線ベクトル)
曲面
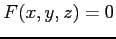 上の曲線を
パラメータ表示して
上の曲線を
パラメータ表示して
 とおく.
このとき,
とおく.
このとき,
が成り立つ.両辺を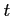 で微分すると
で微分すると
となる.ベクトル表記すると
である. は
曲線
は
曲線
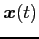 の接ベクトルと常に直交する.
の接ベクトルと常に直交する.
が成り立つ.両辺を
| 0 |  |
|
となる.ベクトル表記すると
である.
曲面 ![]() 上の点
上の点 ![]() において,
この点を通るあらゆる曲線
において,
この点を通るあらゆる曲線
![]() を考える.
便宜上
を考える.
便宜上 ![]() ,
, ![]() ,
, ![]() とおく.
あるベクトル
とおく.
あるベクトル ![]() が
この曲線の接ベクトル
が
この曲線の接ベクトル
![]() と常に直交するとする.
このとき,
と常に直交するとする.
このとき,![]() を
曲面
を
曲面 ![]() の法線ベクトルという.
曲線の接ベクトル
の法線ベクトルという.
曲線の接ベクトル
![]() に
直交するベクトルは
に
直交するベクトルは ![]() であるから,
法線ベクトルは
であるから,
法線ベクトルは
![]() である.
である.
定理 2.184 (接平面)
曲面
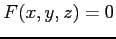 の点
の点  における
接平面(tangent plane)は
における
接平面(tangent plane)は
で与えられる.ベクトルで表記すると
となる.
で与えられる.ベクトルで表記すると
となる.
注意 2.185 (接平面)
グラフ 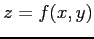 の点
の点 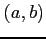 における接平面は,
における接平面は,
 とおき接平面を求めればよい.
とおき接平面を求めればよい.
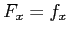 ,
,  ,
,  であるか,
であるか,
となり,接平面は
と表される. この右辺は関数 の
点
の
点 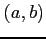 まわりのテイラー展開の 1 次近似と等しい.
まわりのテイラー展開の 1 次近似と等しい.
となり,接平面は
と表される. この右辺は関数
例 2.186 (接平面)
球
 の点
の点
 における
接平面を求める.
における
接平面を求める.
より,接平面は
と求まる. 法線ベクトルが の
平面である.
の
平面である.
より,接平面は
と求まる. 法線ベクトルが
 の
平面である.
の
平面である.
例 2.187 (接平面)
曲面
 の
点
の
点 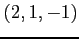 における接平面の方程式を求める.
まず,曲面の方程式を書き直して
における接平面の方程式を求める.
まず,曲面の方程式を書き直して
とする.
より,接平面は
である. 法線ベクトルが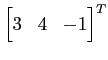 の
平面である.書き直して
の
平面である.書き直して
とする. 平面と 軸,
軸, 軸,
軸, 軸との交点はそれぞれ
軸との交点はそれぞれ
 ,
,  ,
,  である.
である.
とする.
より,接平面は
である. 法線ベクトルが
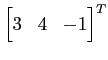 の
平面である.書き直して
の
平面である.書き直して
 |
とする. 平面と
例 2.188 (接平面)
曲面
の点 における接平面を求める.
まず,
における接平面を求める.
まず,
より,接平面は
である. 法線ベクトルが の
平面である.書き直して
の
平面である.書き直して
とする. 平面と 軸,
軸, 軸との交点はぞれぞれ
軸との交点はぞれぞれ  ,
,
 である.
である.
 軸とは交点をもたず,
軸とは交点をもたず,
 軸と平行な平面である.
軸と平行な平面である.
の点
より,接平面は
である. 法線ベクトルが
 の
平面である.書き直して
の
平面である.書き直して
 |
とする. 平面と
例 2.189 (接平面)
関数
 の点
の点  における接平面は,
における接平面は,
より,
と得られる. 接平面を標準形で書くと
である.この平面の法線ベクトルは である.
また,
である.
また,
と書き直す. 平面と 軸,
軸, 軸,
軸, 軸の交点は
軸の交点は
 ,
, 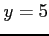 ,
,  である.
である.
より,
と得られる. 接平面を標準形で書くと
である.この平面の法線ベクトルは
 である.
また,
である.
また,
 |
と書き直す. 平面と
平成21年12月2日