2.44 1 変数関数の極値
定義 2.200 (極値)
関数 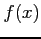 が,
点
が,
点 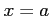 とその任意の近傍の点
とその任意の近傍の点 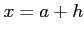 に対して
に対して
をみたすとき,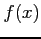 は点
は点 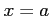 で
極大値
で
極大値  をとるという.
また,
をとるという.
また,
をみたすとき,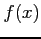 は点
は点 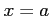 で
極小値
で
極小値  をとるという.
極大値,極小値を総称して極値という.
をとるという.
極大値,極小値を総称して極値という.
をみたすとき,
をみたすとき,
定理 2.201 (極値の必要条件)
関数 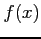 が点
が点 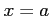 で極値をとるとき,
で極値をとるとき,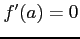 が成り立つ.
(注意)逆は成り立たない.
が成り立つ.
(注意)逆は成り立たない.
となる.これより,
が成り立つ. 右辺の第 1 項目は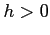 のとき
のとき 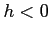 のときで符号が反転し,
右辺全体の符号も反転する.
任意の近傍の点において
のときで符号が反転し,
右辺全体の符号も反転する.
任意の近傍の点において
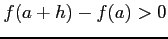 または
または
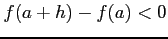 をみたすときのみ極値をとるので,
第 1 項目が 0 となる必要があり,
をみたすときのみ極値をとるので,
第 1 項目が 0 となる必要があり,
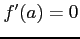 が極値をもつ必要条件となる.
が極値をもつ必要条件となる.
(証明)
関数 ![]() を点
を点 ![]() のまわりで
のまわりで ![]() についてテイラー展開すると,
についてテイラー展開すると,
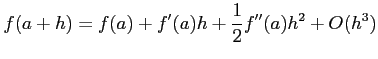 |
となる.これより,
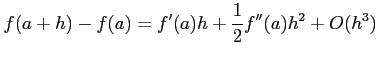 |
が成り立つ. 右辺の第 1 項目は
定理 2.202 (極大,極小)
関数 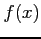 が点
が点 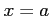 において,
において,
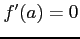 ,
, 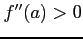 をみたすとき
をみたすとき
 は極小値となる.
は極小値となる.
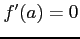 ,
, 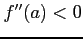 をみたすとき
をみたすとき
 は極大値となる.
(注意)
は極大値となる.
(注意) のときは別途調べる.
のときは別途調べる.
(証明) 前述の定理より明らか.
例 2.203 (極値)
関数
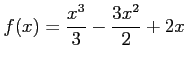 の極値を考える.
の極値を考える.
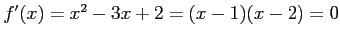 より
より
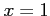 ,
,  が極値をもつ候補の点となる.
が極値をもつ候補の点となる.
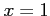 と
と  のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.これより,それぞれ
を得る. よって,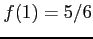 は極大値,
は極大値,
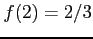 は極小値となる.
は極小値となる.
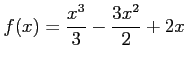 の極値を考える.
の極値を考える.
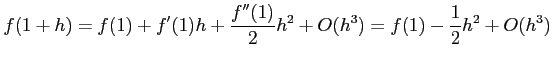 |
||
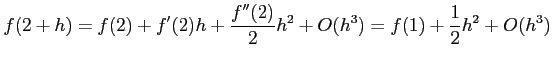 |
となる.これより,それぞれ
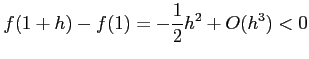 |
||||
 |
を得る. よって,
例 2.204 (極値)
関数  を考える.
を考える.
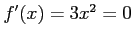 より,
より, が極値の候補となる.
が極値の候補となる.
 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.これより,
が成り立つ.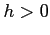 のとき右辺は正,
のとき右辺は正,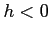 のとき右辺は負となるので,
のとき右辺は負となるので,
 は極値とはならない.
は極値とはならない.
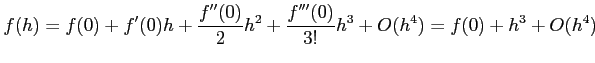 |
となる.これより,
が成り立つ.
例 2.205 (極値)
関数  を考える.
を考える.
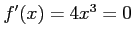 より,
より, が極値の候補となる.
が極値の候補となる.
 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.これより,
が成り立つ. よって,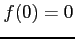 は極小値となる.
は極小値となる.
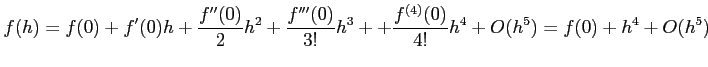 |
となる.これより,
が成り立つ. よって,
平成21年12月2日