2.45 2 変数関数の極値
定義 2.206 (極値)
関数 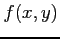 が,
点
が,
点 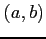 とその任意の近傍の点
とその任意の近傍の点 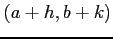 に対して
に対して
をみたすとき,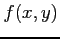 は点
は点 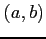 で
極大値
で
極大値 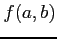 をとるという.
また,
をとるという.
また,
をみたすとき,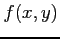 は点
は点 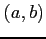 で
極小値
で
極小値 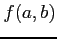 をとるという.
極大値,極小値を総称して極値という.
をとるという.
極大値,極小値を総称して極値という.
をみたすとき,
をみたすとき,
定理 2.207 (極値の必用条件)
関数 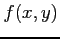 が点
が点 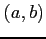 で極値をとるとき,
で極値をとるとき,
が成り立つ. (注意)逆は成り立たない.
が成り立つ. (注意)逆は成り立たない.
(証明)
平面 ![]() と曲面
と曲面 ![]() との共有点からなる曲線
との共有点からなる曲線 ![]() は
は
![]() についての 1 変数関数であり,
についての 1 変数関数であり,
![]() が極値をとるとき
が極値をとるとき ![]() も極値をとる.
よって,
も極値をとる.
よって,
![]() となる.
同様にして,平面
となる.
同様にして,平面 ![]() を考えると
を考えると
![]() を得る.
を得る.
注意 2.208 (極値と接平面)
関数 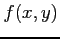 は点
は点 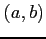 で極値をとるとする.
このとき
で極値をとるとする.
このとき
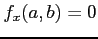 ,
,
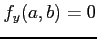 であるから,
であるから,
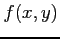 を点
を点 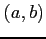 のまわりでテイラー展開すると
のまわりでテイラー展開すると
となり,1 次の項は存在しない. また, 曲面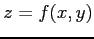 の点
の点 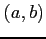 における接平面の方程式は
における接平面の方程式は
となり,法線ベクトルは
である.接平面は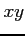 平面に平行である.
平面に平行である.
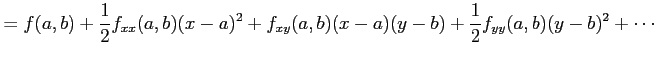 |
となり,1 次の項は存在しない. また, 曲面
となり,法線ベクトルは
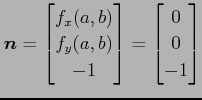 |
である.接平面は
例 2.209 (極値の計算例)
関数
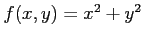 の極値を考える.
連立方程式
の極値を考える.
連立方程式
を解くと候補の点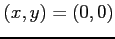 を得る.
このとき点
を得る.
このとき点 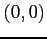 とその任意の近傍の点
とその任意の近傍の点 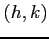 に対して,
に対して,
が成り立つ. よって関数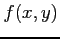 は極小値
は極小値 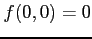 をとる.
をとる.
を解くと候補の点
が成り立つ. よって関数
例 2.210 (極値の計算例)
関数
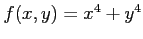 の極値を考える.
連立方程式
の極値を考える.
連立方程式
を解くと候補の点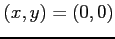 を得る.
このとき点
を得る.
このとき点 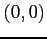 とその任意の近傍の点
とその任意の近傍の点 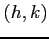 に対して,
に対して,
が成り立つ. よって関数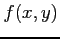 は極小値
は極小値 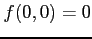 をとる.
をとる.
を解くと候補の点
が成り立つ. よって関数
例 2.211 (鞍点)
関数
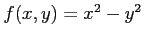 の極値を考える.
連立方程式
の極値を考える.
連立方程式
を解くと候補の点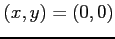 を得る.
このとき,
を得る.
このとき,
が成り立つ. 点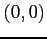 と
と 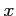 軸方向にずれた近傍の点
軸方向にずれた近傍の点 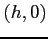 に対しては,
に対しては,
となり,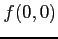 は極小となる.
一方,
点
は極小となる.
一方,
点 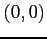 と
と 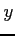 軸方向にずれた近傍の点
軸方向にずれた近傍の点 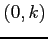 に対しては,
に対しては,
となり,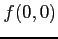 は極大となる.
よって,
は極大となる.
よって,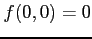 は極値とはならない.
このようにある方向では極小であり,
また別の方向では極大となる点のことを
鞍点(saddle point)という.
は極値とはならない.
このようにある方向では極小であり,
また別の方向では極大となる点のことを
鞍点(saddle point)という.
![\includegraphics[width=0.7\textwidth]{saddle.eps}](img1669.png)
を解くと候補の点
が成り立つ. 点
となり,
となり,
![\includegraphics[width=0.7\textwidth]{saddle.eps}](img1669.png)
例 2.212 (極値の計算例)
関数
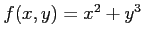 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として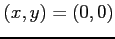 を得る.このとき,
を得る.このとき,
が成り立つ.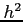 は常に正であるが,
は常に正であるが,
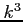 は
は 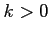 のとき正,
のとき正,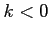 のとき負となる.
右辺全体では正,負が決定しない.
よって,
のとき負となる.
右辺全体では正,負が決定しない.
よって,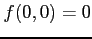 は極値ではない.
は極値ではない.
を解くと極値の候補として
が成り立つ.
例 2.213 (極値の計算例)
関数
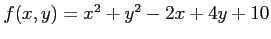 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解くと極値の候補として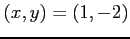 を得る.
を得る.
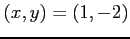 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.よって,
が成り立つ.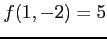 は極小値となる.
は極小値となる.
を解くと極値の候補として
となる.よって,
が成り立つ.
例 2.214 (極値の計算例)
関数
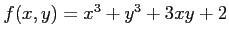 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解く. 第 1 式を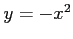 と変形して第 2 式に代入すると
と変形して第 2 式に代入すると
となる.これを解くと,極値の候補として
を得る.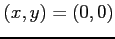 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.よって,
の右辺は ,
, 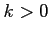 のときは正,
のときは正,
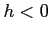 ,
, 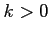 のときは負となり,
符号が定まらない.
のときは負となり,
符号が定まらない.
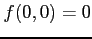 は極値ではない.
は極値ではない.
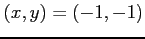 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる. これより,
が成り立つ.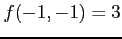 は極大値となる.
は極大値となる.
を解く. 第 1 式を
となる.これを解くと,極値の候補として
を得る.
となる.よって,
の右辺は
となる. これより,
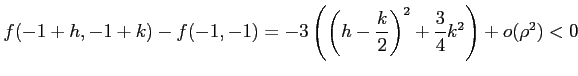 |
||
が成り立つ.
例 2.215 (極値の計算例)
関数
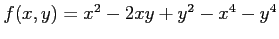 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解く. 第 1 式と第 2 式を足し合わせると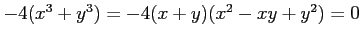 であるから,
であるから,
 である.
これを第 1 式に代入すると,
である.
これを第 1 式に代入すると,
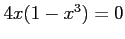 であるから,
であるから,
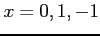 となる.
よって,極値の候補は
となる.
よって,極値の候補は
である. それぞれの点のまわりで 2 次までテイラー展開する.
より,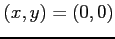 のときは,
のときは,
となる. よって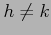 のときは
のときは
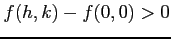 が成立する.
が成立する.
 のときは 2 次の項が消えるので,
さらに高次の項まで展開する必要がある.
のときは 2 次の項が消えるので,
さらに高次の項まで展開する必要がある.
より, 4 次の項まで展開すると,
となる. のとき,
のとき,
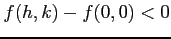 が成立する.
が成立する.
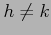 と
と  のときでは符号が異なるので,
のときでは符号が異なるので,
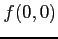 は極値ではない.
次に,
は極値ではない.
次に,
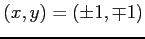 (復号同順)のときは,
(復号同順)のときは,
となる. よって,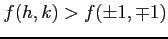 が成立し,
が成立し,
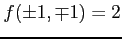 は極大値となる.
は極大値となる.
を解く. 第 1 式と第 2 式を足し合わせると
である. それぞれの点のまわりで 2 次までテイラー展開する.
より,
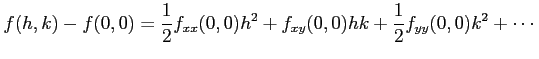 |
||
となる. よって
より, 4 次の項まで展開すると,
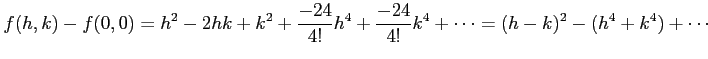 |
となる.
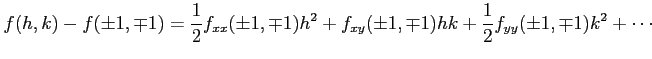 |
||
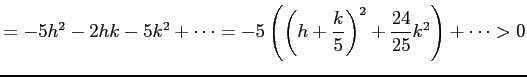 |
となる. よって,
例 2.216 (極値の計算例)
関数
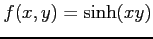 の極値を求める.
連立方程式
の極値を求める.
連立方程式
を解く.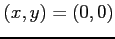 が極値の候補となる.
が極値の候補となる.
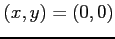 のまわりでテイラー展開すると,
のまわりでテイラー展開すると,
となる.よって,
の右辺の符号は定まらない.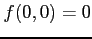 は極値ではない.
は極値ではない.
を解く.
となる.よって,
の右辺の符号は定まらない.
平成21年12月2日