2.48 条件付き極値問題
例 2.223 (条件付き極値)
条件
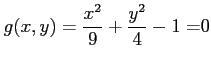 のもとでの
関数
のもとでの
関数
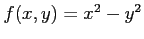 の極値を求める.
条件
の極値を求める.
条件 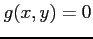 は楕円の方程式であるから,
は楕円の方程式であるから,
 ,
,  は
は
とパラメータ表示で表される. このとき当然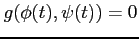 が成立する.
が成立する.
 ,
,  は
は 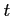 の関数であるから,
の関数であるから,
 も
も 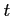 の関数となり,
の関数となり,
と書ける. 求めるべき極値は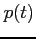 の極値を求めればよい.
の極値を求めればよい.
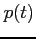 を式変形すると,
を式変形すると,
であり,この導関数は
となる. のとき極値の候補となる.
のとき極値の候補となる.
 に注意すると,
に注意すると,
 のときが極値に候補となる.
のときが極値に候補となる.
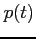 の 2 階の導関数は
の 2 階の導関数は
であるから, のとき
のとき
 となるので,
となるので,
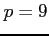 は極大値となる.
は極大値となる.
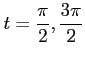 のとき
のとき
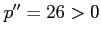 となるので,
となるので,
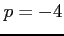 は極小値となる.
よって,
は極小値となる.
よって,
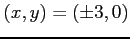 のとき
極大値
のとき
極大値
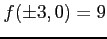 をとり,
をとり,
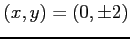 のとき
極大値
のとき
極大値
 をとる.
をとる.
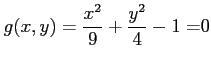 のもとでの
関数
のもとでの
関数
とパラメータ表示で表される. このとき当然
と書ける. 求めるべき極値は
であり,この導関数は
となる.
 のときが極値に候補となる.
のときが極値に候補となる.
であるから,
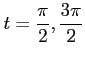 のとき
のとき
例 2.224 (条件付き極値)
条件
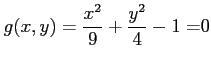 のもとでの
関数
のもとでの
関数
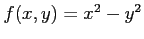 の極値を求める.
条件
の極値を求める.
条件 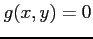 により定まる 2 つの
陰関数をそれぞれ
により定まる 2 つの
陰関数をそれぞれ
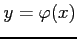 ,
, 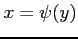 とおく.
これらの導関数は
とおく.
これらの導関数は
となる. また,合成関数 ,
,
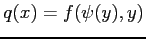 の
導関数はそれぞれ
の
導関数はそれぞれ
となる. 極値の候補となる点は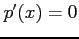 ,
,
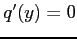 をみたす点である.
これらよりそれぞれ
をみたす点である.
これらよりそれぞれ  ,
, 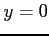 を得る.
このとき
を得る.
このとき 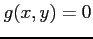 を代入すると
ぞれぞれ,
を代入すると
ぞれぞれ,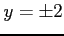 ,
, 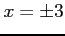 を得る.
よって,極値の候補は
を得る.
よって,極値の候補は
である. これらの点が極値であるか確認する. さらに微分すると
となる. よって,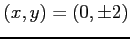 のとき,
のとき, となるから
となるから  を用いて
を用いて
となるので, は極小値である.
また,
は極小値である.
また,
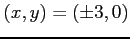 のとき,
のとき,
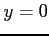 となるから
となるから 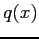 を用いて
を用いて
となるので,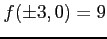 は極大値である.
は極大値である.
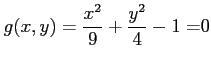 のもとでの
関数
のもとでの
関数
 ただし ただし |
||
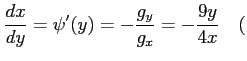 ただし ただし |
となる. また,合成関数
 |
||
 ただし ただし |
||
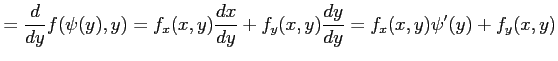 |
||
 ただし ただし |
となる. 極値の候補となる点は
である. これらの点が極値であるか確認する. さらに微分すると
 ただし ただし |
||
 ただし ただし |
となる. よって,
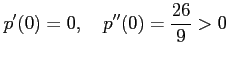 |
となるので,
 |
となるので,
例 2.225 (条件付き極値)
条件
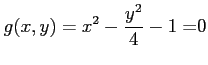 のもとでの
関数
のもとでの
関数
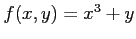 の極値を求める.
条件
の極値を求める.
条件 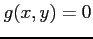 により定まる陰関数を
により定まる陰関数を
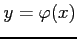 とおく.
この導関数は
とおく.
この導関数は
となる. また,合成関数 の導関数は
の導関数は 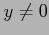 のとき
のとき
となる. 極値の候補は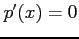 となる点である.
これより,
となる点である.
これより,
を得る. これを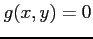 へ代入すると,
へ代入すると,
となる. とおけば
とおけば
となるので,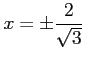 を得る.
よって,極値の候補となる点は
を得る.
よって,極値の候補となる点は
である. これらの点が極値であるか確認する. をさらに微分すると
をさらに微分すると
となる. よって,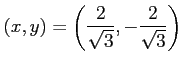 のとき,
のとき,
となるので,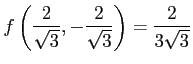 は極小値であり,
は極小値であり,
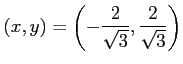 のとき,
のとき,
となるので,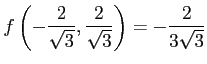 は極大値である.
は極大値である.
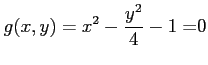 のもとでの
関数
のもとでの
関数
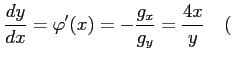 ただし ただし |
となる. また,合成関数
 |
となる. 極値の候補は
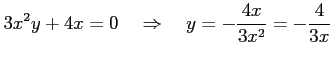 |
を得る. これを
となる.
となるので,
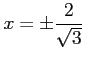 を得る.
よって,極値の候補となる点は
を得る.
よって,極値の候補となる点は
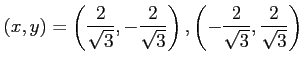 |
である. これらの点が極値であるか確認する.
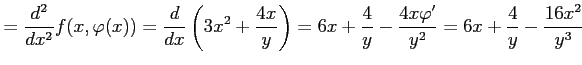 |
||
 |
となる. よって,
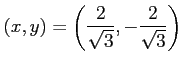 のとき,
のとき,
 |
となるので,
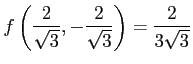 は極小値であり,
は極小値であり,
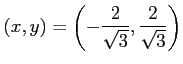 のとき,
のとき,
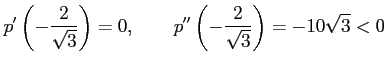 |
となるので,
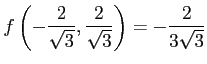 は極大値である.
は極大値である.
例 2.226 (条件付き極値)
条件
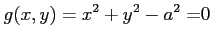 (
(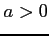 ) のもとでの
関数
) のもとでの
関数
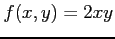 の極値を求める.
条件
の極値を求める.
条件 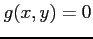 により定まる陰関数を
により定まる陰関数を
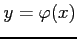 とおく.
この導関数は
とおく.
この導関数は
となる. また,合成関数 の導関数は
の導関数は 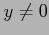 のとき
のとき
となる.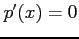 をみたす点が極値の候補である.
これより
をみたす点が極値の候補である.
これより 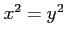 を得る.
を得る.
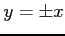 を
を 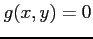 へ代入すると,
へ代入すると,
 となり,
となり,
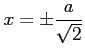 であるから,
極値の候補となる点は
であるから,
極値の候補となる点は
である. これらの点が極値であるか確認する. をさらに微分すると
をさらに微分すると
となる. よって,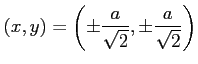 のとき,
のとき,
となるので,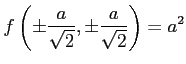 は極大値である.
は極大値である.
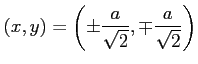 のとき,
のとき,
となるので,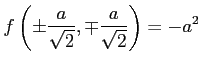 は極小値である.
は極小値である.
 ただし ただし |
となる. また,合成関数
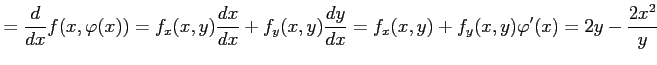 |
となる.
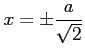 であるから,
極値の候補となる点は
であるから,
極値の候補となる点は
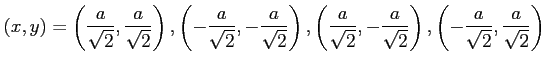 |
である. これらの点が極値であるか確認する.
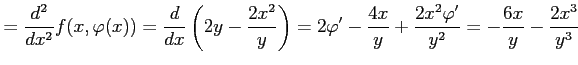 |
となる. よって,
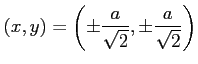 のとき,
のとき,
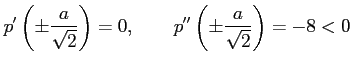 |
となるので,
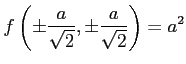 は極大値である.
は極大値である.
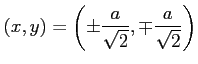 のとき,
のとき,
 |
となるので,
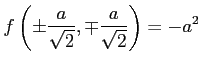 は極小値である.
は極小値である.
平成21年12月2日