5.4 行列の固有値
線形変換
![]() ;
;
![]() に関する固有値
に関する固有値 ![]() を定める.
固有方程式は
を定める.
固有方程式は
![]() より
より
となる.これを変形して
となる. 同次系であるから自明な解
であればよい. これと必要十分な条件は
である. 方程式(☆)により固有値
定義 5.10 (固有多項式)
正方行列  に対して
に対して
を行列 の固有多項式(eigen-polynomial)または
特性多項式(characteristic polynomial)という.
の固有多項式(eigen-polynomial)または
特性多項式(characteristic polynomial)という.
を行列
定義 5.11 (行列の固有値)
行列  に対する固有多項式
に対する固有多項式 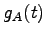 の根を
(複素数も含めて)行列
の根を
(複素数も含めて)行列  の固有値という.
の固有値という.
注意 5.12 (行列の固有値の個数)
正方行列
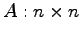 の固有値の個数は
重複を別のもととして数えると
の固有値の個数は
重複を別のもととして数えると 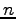 個である.
個である.
定理 5.13 (線形変換の固有値と行列の固有値)
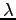 が線形変換
が線形変換  の固有値であることと,
の固有値であることと,
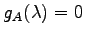 が成り立つこととは,
必要十分条件である.
が成り立つこととは,
必要十分条件である.
例 5.14 (行列の固有値の具体例)
行列
の固有多項式は
である. よって の固有値は
の固有値は
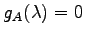 より
より
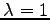 と
と 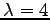 である.
である.
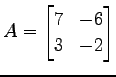 |
の固有多項式は
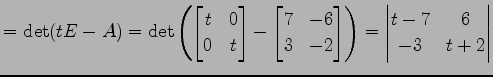 |
||
である. よって
線形変換
![]() ;
;
![]() の
固有値は
の
固有値は ![]() と
と ![]() である.
である.
例 5.15 (行列の固有値の具体例)
行列
の固有多項式は
である. よって の固有値は
の固有値は
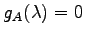 より
より
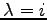 と
と
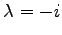 である.
である.
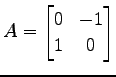 |
の固有多項式は
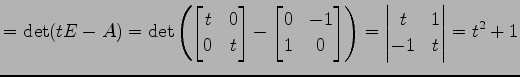 |
である. よって
線形変換
![]() ;
;
![]() の
固有値は存在しない.
しかし,線形変換
の
固有値は存在しない.
しかし,線形変換
![]() ;
;
![]() の
固有値は
の
固有値は ![]() と
と
![]() である.
である.
平成20年2月2日