5.5
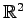 における線形変換の固有空間
における線形変換の固有空間
例 5.16 (線形変換の固有空間の具体例)
線形変換
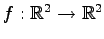 ;
;
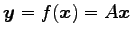 の固有空間を求める.
ただし,
の固有空間を求める.
ただし,
とする. まず,固有多項式は
である.よって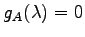 より
固有値は
より
固有値は
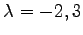 である.
である.
となる.これより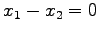 であるから解は
であるから解は
となる.ただし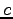 は任意定数である.
よって
は任意定数である.
よって
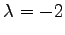 に属する固有ベクトルは
に属する固有ベクトルは
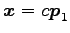 (
(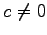 ) である.
また,固有空間は固有ベクトル全体の集合に
) である.
また,固有空間は固有ベクトル全体の集合に 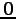 を
加えたものであるから,
を
加えたものであるから,
となる.
となる.これより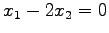 であるから解は
であるから解は
となる.ただし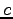 は任意定数である.
よって
は任意定数である.
よって 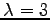 に属する固有ベクトルは
に属する固有ベクトルは
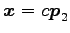 (
(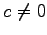 ) である.
また,固有空間は固有ベクトル全体の集合に
) である.
また,固有空間は固有ベクトル全体の集合に 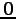 を
加えたものであるから,
を
加えたものであるから,
となる.
より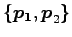 は 1 次独立であるから,
は 1 次独立であるから,
となる.よって,
が成り立つ.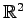 は
は 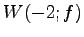 と
と 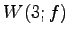 に直和分解される.
に直和分解される.
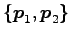 は
は
 の基底となる.
の基底となる.
と座標変換が得られる. これを用いて, 線形変換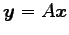 を座標変換すると
を座標変換すると
と表される. よって,基底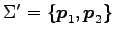 に関する
に関する
 の表現行列は
の表現行列は
となる. あらたな座標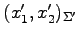 のもとでの
のもとでの
 は
は
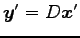 より
より
と表される. また,これは次のようにも示される.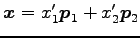 を
を  で変換すると
で変換すると
となる.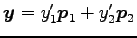 より,
より,
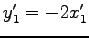 ,
,
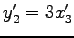 を得る.
を得る.
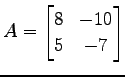 |
とする. まず,固有多項式は
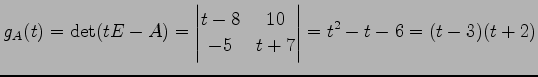 |
である.よって
固有ベクトルをそれぞれ求める.
![]() のとき
のとき
![]() より
方程式
より
方程式
![]() をみたす
をみたす ![]() を求める.
行列
を求める.
行列 ![]() を簡約化すると
を簡約化すると
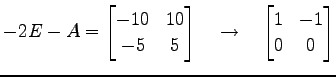 |
となる.これより
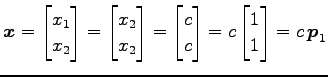 |
となる.ただし
となる.
![]() のとき
のとき
![]() より
方程式
より
方程式
![]() をみたす
をみたす ![]() を求める.
行列
を求める.
行列 ![]() を簡約化すると
を簡約化すると
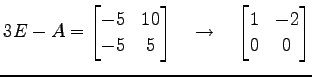 |
となる.これより
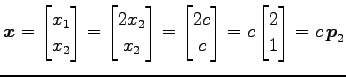 |
となる.ただし
となる.
固有空間 ![]() の基底は
の基底は
![]() であり
であり
![]() となる.
固有空間
となる.
固有空間 ![]() の基底は
の基底は
![]() であり
であり
![]() となる.
また,
となる.
また,
 |
より
となる.よって,
が成り立つ.
標準基底
![]() に関する
に関する ![]() の
表現行列は
の
表現行列は ![]() である.
基底
である.
基底
![]() に関する
に関する ![]() の
表現行列を求める.
の
表現行列を求める.
![]() ,
, ![]() の座標を
の座標を
![]() ,
,
![]() とすると,
とすると,
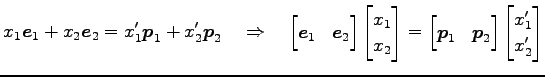 |
||
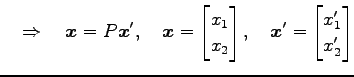 |
と座標変換が得られる. これを用いて, 線形変換
と表される. よって,基底
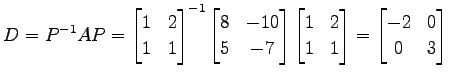 |
となる. あらたな座標
と表される. また,これは次のようにも示される.
となる.
平成20年2月2日