5.11 対角行列の固有値
定理 5.31 (固有値)
上三角行列
下三角行列
対角行列
の固有値はいずれも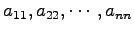 である.
である.
であり,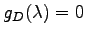 より
固有値
より
固有値
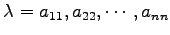 を得る.
を得る.
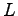 ,
, 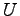 についても同様である.
についても同様である.
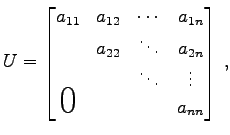 |
下三角行列
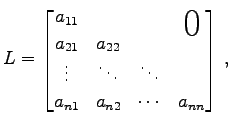 |
対角行列
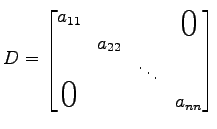 |
の固有値はいずれも
(証明)
![]() の固有多項式は
の固有多項式は
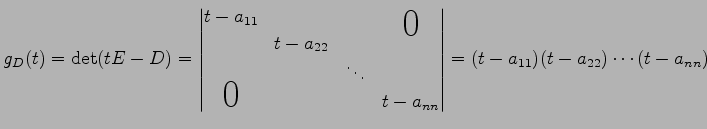 |
であり,
平成20年2月2日