5.14 行列の対角化
定義 5.37 (対角化)
正方行列 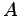 を相似変換により対角行列
を相似変換により対角行列 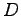 に変換することを
対角化という.
すなわち,
に変換することを
対角化という.
すなわち,
をみたす対角行列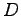 と正則行列
と正則行列 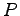 を
定めることを対角化いう.
を
定めることを対角化いう.
をみたす対角行列
![]() ,
,
![]() が存在するとき,
が存在するとき,
![]() は実数体上で対角化されるという.
は実数体上で対角化されるという.
![]() ,
,
![]() が存在するとき,
が存在するとき,
![]() は複素数体上で対角化されるという.
は複素数体上で対角化されるという.
注意 5.38 (対角化)
正方行列 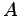 は常に対角化可能とは限らない.
は常に対角化可能とは限らない.
注意 5.39 (対角化と固有値)
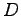 は
は 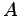 の相似変換により定まるので両者の固有値は等しく,
対角行列
の相似変換により定まるので両者の固有値は等しく,
対角行列
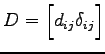 の
対角成分
の
対角成分
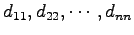 が固有値となる.
なぜなら,
が固有値となる.
なぜなら,
となるからである. よって行列 の固有値を
の固有値を
 とすると
とすると
 は
は
と表される.
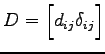 の
対角成分
の
対角成分
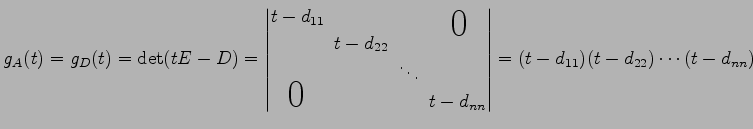 |
となるからである. よって行列
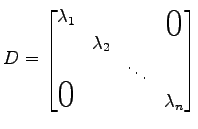 |
と表される.
定義 5.40 (対角行列)
対角行列
を省略記号として
と表す.
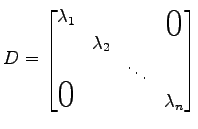 |
を省略記号として
と表す.
行列 ![]() の固有値を
の固有値を
![]() ,
, ![]() ,
, ![]() ,
, ![]() とする.
ただし,重複する固有値は別のものとして考える.
とする.
ただし,重複する固有値は別のものとして考える.
![]() ,
, ![]() ,
, ![]() ,
, ![]() に
属する固有ベクトルをそれぞれ
に
属する固有ベクトルをそれぞれ
![]() ,
, ![]() ,
, ![]() ,
, ![]() とする.
このとき固有方程式
とする.
このとき固有方程式
![]() より
より
が成り立つ. これを列ベクトルとして並べると
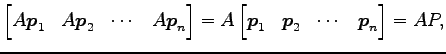 |
||
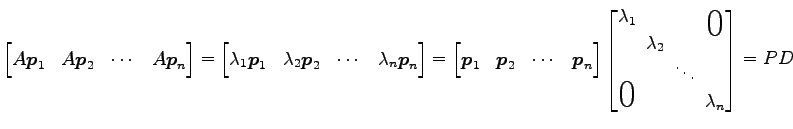 |
となる. これより
が成り立つ.
定理 5.41 (対角化)
正方行列 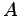 の固有値を
の固有値を
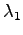 ,
, 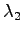 ,
,  ,
, 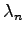 とし,
その固有ベクトルをそれぞれ
とし,
その固有ベクトルをそれぞれ
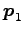 ,
, 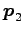 ,
,  ,
, 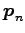 とする.
とする.
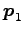 ,
, 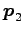 ,
,  ,
, 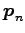 が
1 次独立であるとき,
が
1 次独立であるとき,
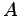 は
は
により対角化される.
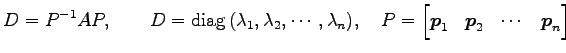 |
により対角化される.
定理 5.42 (固有ベクトルの 1 次独立性)
固有値 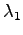 ,
,  ,
, 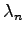 が
互いに異なるとき,
固有ベクトル
が
互いに異なるとき,
固有ベクトル 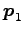 ,
,  ,
, 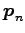 は
1 次独立である.
は
1 次独立である.
と書ける. 両辺に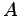 を掛けると
を掛けると
となる. また,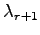 を掛けると
を掛けると
となる. これらを差引すると
を得る. これは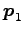 ,
,  ,
, 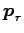 の 1 次関係である.
の 1 次関係である.
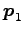 ,
,  ,
, 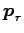 は 1 次独立であり,
固有値は互いに異なる
は 1 次独立であり,
固有値は互いに異なる
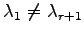 ,
,
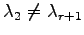 ,
,
 ,
,
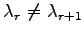 ので,
ので,
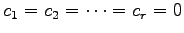 となる.
このとき
となる.
このとき
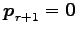 である.
固有値は零ベクトルとはならないので,
条件は矛盾する.
よって,
である.
固有値は零ベクトルとはならないので,
条件は矛盾する.
よって,
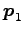 ,
,  ,
, 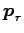 ,
,
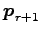 は
1 次独立である.
すべての
は
1 次独立である.
すべての
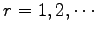 対して成り立つので
対して成り立つので 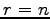 を得る.
を得る.
(証明)
![]() ,
, ![]() ,
, ![]() の
1 次独立なベクトルの最大個数を
の
1 次独立なベクトルの最大個数を ![]() とする.
とする.
![]() ,
, ![]() ,
, ![]() を
1 次独立とし,
を
1 次独立とし,
![]() ,
, ![]() ,
, ![]() ,
,
![]() を
1 次従属とする.
このとき
を
1 次従属とする.
このとき
と書ける. 両辺に
となる. また,
となる. これらを差引すると
を得る. これは
平成20年2月2日