5.16 対角化によるべき行列の計算
例 5.47 (対角化の応用例)
行列  が
が
と対角化可能であるとする. このとき,左から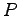 を掛けて,右から
を掛けて,右から 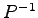 を掛けると
を掛けると
となる. これを用いるとべき行列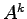 は
は
と得られる. ここで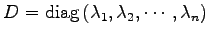 おくと,
おくと,
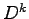 は
は
と表される. よって
となる.
と対角化可能であるとする. このとき,左から
となる. これを用いるとべき行列
と得られる. ここで
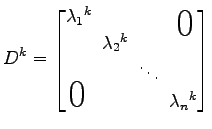 |
と表される. よって
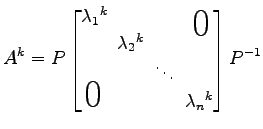 |
となる.
例 5.48 (べき行列の具体例)
行列
は
と対角化される. これより
を得る.
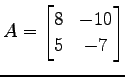 |
は
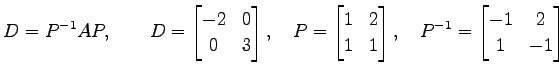 |
と対角化される. これより
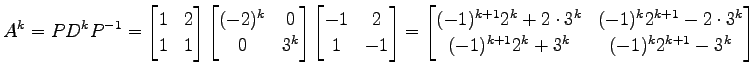 |
を得る.
平成20年2月2日