5.17 3 次正方行列の対角化
例 5.49 (対角化の具体例)
行列
を対角化する.
であるから, 固有値は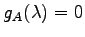 より
より
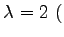 2 重
2 重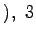 となる.
となる.
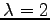 のとき,
のとき,
となるので,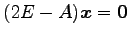 を解いて
固有ベクトルは
を解いて
固有ベクトルは
と得られる.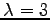 のとき,
のとき,
となるので,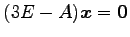 を解いて
固有ベクトルは
を解いて
固有ベクトルは
と得られる.
と選ぶ. このとき, 同じ固有値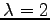 に属する
固有ベクトル
に属する
固有ベクトル 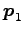 ,
, 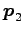 を選ぶときは,
1 次独立となるよう選ぶ.
以上より,
を選ぶときは,
1 次独立となるよう選ぶ.
以上より,
とおくと,行列 は
は
と対角化される.
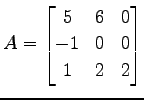 |
を対角化する.
まず,行列 ![]() の固有多項式は
の固有多項式は
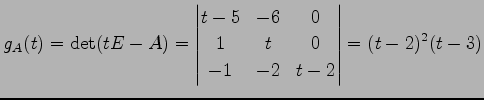 |
であるから, 固有値は
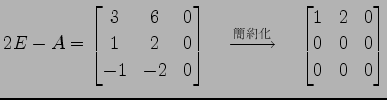 |
となるので,
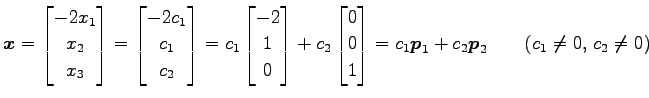 |
と得られる.
 |
となるので,
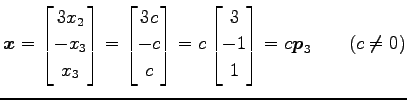 |
と得られる.
行列 ![]() を対角化する.
重複する固有値は別のものとして考えて,
三つの固有値を
を対角化する.
重複する固有値は別のものとして考えて,
三つの固有値を
![]() ,
,
![]() ,
,
![]() とおく.
それぞれの固有値に属する固有ベクトルを
とおく.
それぞれの固有値に属する固有ベクトルを
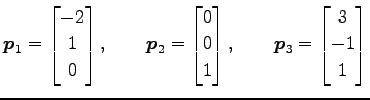 |
と選ぶ. このとき, 同じ固有値
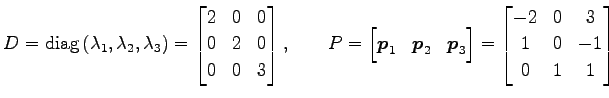 |
とおくと,行列
と対角化される.
注意 5.50 (対角化の任意性)
 ,
,  ,
, 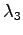 の
取り方の順には自由度がある.
固有値の取り方にもスカラー倍の自由度がある.
よって
の
取り方の順には自由度がある.
固有値の取り方にもスカラー倍の自由度がある.
よって 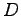 ,
, 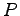 は一通りに定まるわけではない.
は一通りに定まるわけではない.
注意 5.51 (固有空間による直和分解)
線形変換
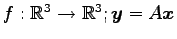 の固有空間は
の固有空間は
である.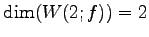 ,
,
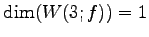 ,
,
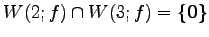 となるので,
となるので,
が成り立つ.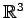 は固有空間に直和分解される.
は固有空間に直和分解される.
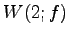 の基底は
の基底は
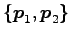 ,
,
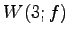 の基底は
の基底は
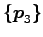 ,
,
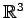 の基底は
の基底は
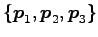 となる.
となる.
である.
が成り立つ.
問 5.52 (固有空間)
固有空間 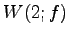 は原点を通り法線ベクトル
は原点を通り法線ベクトル
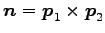 の平面であり,
固有空間
の平面であり,
固有空間 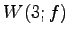 は原点を通り方向ベクトル
は原点を通り方向ベクトル
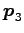 の直線である.
直線と平面のなす角度の最小値を求めよ.
の直線である.
直線と平面のなす角度の最小値を求めよ.
平成20年2月2日