5.19 ちょっとまとめ
注意 5.55 (複素体上の対角化)
複素数体上の場合でも対角化の手順は同じである.
行列  の固有値が
の固有値が
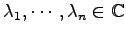 であり,
固有ベクトルが
であり,
固有ベクトルが
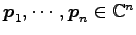 のとき,
のとき,
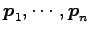 が 1 次独立であれば,
が 1 次独立であれば,
と対角化可能である.
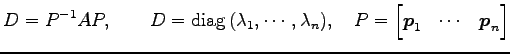 |
と対角化可能である.
まとめ 5.56 (対角化)
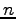 次正方行列
次正方行列  の固有値を重複は別のものとして
の固有値を重複は別のものとして
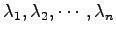 とする.
この固有値に属する固有ベクトルをそれぞれ
とする.
この固有値に属する固有ベクトルをそれぞれ
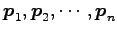 とする.
また,重複する固有値を同じものとして
とする.
また,重複する固有値を同じものとして
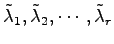 (
(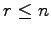 ) とする.
) とする.
 は線形変換
は線形変換
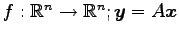 とする.
とする.
- (1)
-
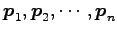 が 1 次独立のとき.
すなわち,
が 1 次独立のとき.
すなわち,
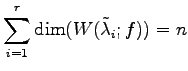 のとき.
のとき.
- (i)
-
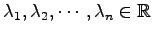 のとき.
のとき.
- (a)
- 実数体上で対角化可能である.
- (ii)
-
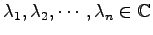 のとき.
のとき.
- (b)
- 複素数体上で対角化可能である.
- (c)
- 実数体上では対角化不可能である. しかし,実標準形には分解可能である.
- (2)
-
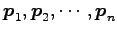 が 1 次従属のとき.
すなわち,
が 1 次従属のとき.
すなわち,
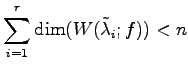 のとき.
のとき.
- (d)
- 行列
 は対角化不可能である.
しかし,ジョルダン標準形には分解可能である.
は対角化不可能である.
しかし,ジョルダン標準形には分解可能である.
平成20年2月2日