5.20 対角化と座標変換
線形変換
![]() ;
;
において, 行列
と書ける. 両辺に左から
となる. これを(☆)へ代入すると
となる.ここで
とおくと,
を得る. (♭)は
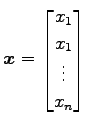 |
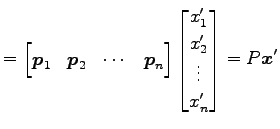 |
|
と表されるので, (♭)は 標準基底
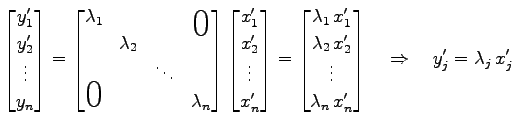 |
となる. 各座標
平成20年2月2日
5.20 対角化と座標変換
線形変換
;
☆
において, 行列は対角化可能であるとすると,
と書ける. 両辺に左からを掛け,右からから
を掛けると
となる. これを(☆)へ代入すると
となる.ここで
♭
とおくと,
★
を得る. (♭)は
と表されるので, (♭)は 標準基底における座標
と 基底
における座標
との 座標変換とみなせる.
,
についても同様である. よって(★)は 固有ベクトル
を基底とするあらたな座標系における 線形変換
であり,あらためて成分で書くと
となる. 各座標が独立して, スカラー倍される単純な変換
とみなされる.
平成20年2月2日